上位10個の検索語を見つけるアルゴリズム
現在、インタビューの準備をしていますが、以前のインタビューで次のような質問があったことを思い出しました。
「Googleの検索キーワード上位10を継続的に表示するソフトウェアを設計するように求められました。Googleで現在検索されている検索キーワードの無限のリアルタイムストリームを提供するフィードにアクセスできます。どのアルゴリズムとデータ構造を説明しますこれを実装するために使用します。次の2つのバリエーションを設計します。
(i)常にトップ10の検索用語を表示します(つまり、フィードの読み取りを開始してから)。
(ii)毎月更新された過去1か月の上位10個の検索語のみを表示します。
近似値を使用してトップ10リストを取得できますが、選択を正当化する必要があります。」
私はこのインタビューで爆弾を投じましたが、これをどのように実装するかはまだまったく分かりません。
最初の部分では、無限リストの継続的に成長するサブシーケンスで最も頻繁に使用される10個の項目を要求します。選択アルゴリズムを調べましたが、この問題を解決するためのオンラインバージョンが見つかりませんでした。
2番目の部分は有限リストを使用しますが、大量のデータが処理されるため、実際には1か月分の検索用語をメモリに保存し、1時間ごとにヒストグラムを計算することはできません。
この問題は、トップ10リストが継続的に更新されているため、さらに困難になっています。そのため、スライディングウィンドウでトップ10を計算する必要があります。
何か案は?
まあ、非常に多くのデータのように見えますが、おそらくすべての周波数を保存するのに法外なコストがかかります。 データの量が非常に多いため、すべてを保存することを期待できない場合、dataのドメインを入力しますストリームアルゴリズム。
この分野で役立つ本: Muthukrishnan-"データストリーム:アルゴリズムとアプリケーション"
上記から選んだ当面の問題への密接に関連する参照: Manku、Motwani-"データストリームの概算周波数カウント" [pdf]
ところで、スタンフォードのMotwani(編集)は非常に重要な "Randomized Algorithms" 本の著者でした。 この本の第11章はこの問題を扱っています。 編集:申し訳ありませんが、悪い章です。その章は別の問題を扱っています。確認後、代わりに Muthukrishnanの本のセクション5.1.2 をお勧めします。オンラインで入手できます。
へー、ニースのインタビューの質問。
周波数推定の概要
一定量のストレージを使用して、このようなストリームの周波数推定値を提供できるいくつかの有名なアルゴリズムがあります。 1つは、Misra and Gries(1982)によるFrequent、です。 nアイテムのリストから、k-1カウンターを使用して、n/k回以上発生するすべてのアイテムを検索します。これはボイヤーとムーアのMajorityアルゴリズム(Fischer-Salzberg、1982)の一般化です。ここでkは2です。MankuとMotwaniのLossyCounting(2002 )およびMetwallyのSpaceSaving(2005)アルゴリズムには同様のスペース要件がありますが、特定の条件下でより正確な推定値を提供できます。
覚えておくべき重要なことは、これらのアルゴリズムは周波数推定のみを提供できるということです。具体的には、Misra-Griesの見積もりでは、(n/k)項目によって実際の頻度を過少カウントできます。
アイテムを確実に識別できるアルゴリズムがあると仮定しますのみ 50%以上の頻度で発生する場合。このアルゴリズムに[〜#〜] n [〜#〜]個別のアイテムのストリームをフィードしてから、別のアイテムを追加しますN-1 1つのアイテムのコピーx、合計2N-1アイテム。アルゴリズムがxが全体の50%を超えることを示している場合、それは最初のストリームにあったに違いありません。そうでない場合、xは初期ストリームにありませんでした。アルゴリズムがこの決定を行うには、初期ストリーム(またはその長さに比例した要約)を保存する必要があります!そのため、このような「正確な」アルゴリズムに必要なスペースがΩ([〜#〜] n [〜#〜])になることを証明できます。
代わりに、ここで説明するこれらの頻度アルゴリズムは、しきい値を超えるアイテムを特定する推定値を提供し、特定のマージンでそれを下回るいくつかのアイテムを識別します。たとえば、単一のカウンタを使用するMajorityアルゴリズムは常に結果を返します。ストリームの50%を超えるアイテムがある場合、そのアイテムが見つかります。ただし、1回だけ発生するアイテムを提供する場合もあります。データの2回目のパスなしではわかりません(再び1つのカウンターを使用しますが、そのアイテムのみを探します)。
頻繁なアルゴリズム
Misra-GriesのFrequentアルゴリズムの簡単な説明を次に示します。 Demaine(2002)などはアルゴリズムを最適化しましたが、これは要点を示しています。
しきい値の割合を指定します1/k; n/k回より多く発生するアイテムが検出されます。空のマップ(赤黒ツリーのような)を作成します。キーは検索語になり、値はその語のカウンターになります。
- ストリーム内の各アイテムを見てください。
- マップに用語が存在する場合、関連するカウンターをインクリメントします。
- それ以外の場合、マップがk-1エントリよりも小さい場合は、カウンタが1の用語をマップに追加します。
- ただし、マップにk-1エントリが既にある場合は、すべてのエントリでカウンタを減らします。このプロセス中にカウンターがゼロになった場合、マップから削除します。
固定量のストレージ(固定サイズのマップのみ)で無限量のデータを処理できることに注意してください。必要なストレージの量は、対象のしきい値のみに依存し、ストリームのサイズは重要ではありません。
検索のカウント
このコンテキストでは、おそらく1時間の検索をバッファリングし、その時間のデータに対してこのプロセスを実行します。この時間の検索ログで2回目のパスを取得できる場合、最初のパスで特定された上位「候補」の正確な発生回数を取得できます。または、単一のパスを作成し、すべての候補者を報告して、そこにあるべきアイテムが含まれており、余分なものは次の1時間で消えるだけのノイズであることを知っていてもよいでしょう。
実際に関心のあるしきい値を超えた候補は、要約として保存されます。これらの要約を1か月分保持し、1時間ごとに最も古いものを破棄すると、最も一般的な検索用語の適切な近似値が得られます。
ハッシュテーブル を バイナリ検索ツリー と組み合わせて使用できます。 <search term, count>各検索語が何回検索されたかを示す辞書。
明らかに、トップ10を取得するためにハッシュテーブル全体を1時間ごとに繰り返すことはveryが悪いです。しかし、これは私たちが話しているグーグルですので、トップ10のすべてがヒットすると仮定することができます。たとえば、ヒット数が10,000を超えると考えられます(ただし、おそらくはるかに大きい数です)。したがって、検索語のカウントが10000を超えるたびに、BSTに挿入します。その後、1時間ごとに、BSTから最初の10個を取得するだけで済みます。これには、比較的少ないエントリが含まれているはずです。
これにより、過去10回のトップ10の問題が解決されます。
本当にトリッキーな部分は、月次レポートである用語を別の用語に置き換えることです(たとえば、「スタックオーバーフロー」は過去2か月で50 000ヒットしますが、「Amazon」は40ヒットしますが、過去2か月間は000でしたが、過去1か月間は30000です。月次レポートで「スタックオーバーフロー」の前に「Amazon」が来るようにします)。これを行うには、すべての主要な(10,000以上の全時間検索)検索用語に対して、その用語が毎日検索された回数を示す30日間のリストを保存します。リストはFIFOキューのように機能します。最初の日を削除し、毎日(または毎時間)新しい日を挿入しますが、より多くの情報を保存する必要がある場合があります。メモリが問題にならない場合はそれを行い、そうでない場合は彼らが話している「概算」に進みます)。
これは良いスタートのようです。その後、ヒット数が10,000を超えているものの、長い間使用していない用語などを削除することを心配することができます。
ケースi)
すべての検索用語のハッシュテーブルと、ハッシュテーブルとは別のソートされたトップ10リストを維持します。検索が発生するたびに、ハッシュテーブル内の適切なアイテムをインクリメントし、そのアイテムがトップ10リストの10番目のアイテムに切り替わるかどうかを確認します。
トップ10リストのO(1)ルックアップ、およびmax O(log(n))ハッシュテーブルへの挿入(自己バランス型バイナリツリーによって管理される衝突を想定))。
case ii)巨大なハッシュテーブルと小さなリストを維持する代わりに、ハッシュテーブルとすべてのアイテムのソートされたリストを維持します。検索が行われるたびに、その用語はハッシュテーブルでインクリメントされ、ソートされたリストで用語をチェックして、その後の用語と切り替える必要があるかどうかを確認できます。自己バランス型のバイナリツリーは、このために適切に機能する可能性があります。これは、クエリを迅速に実行できるようにする必要があるためです(これについては後で説明します)。
さらに、「時間」のリストをFIFO list(queue))の形式で保持します。各「時間」要素には、その特定の時間内に実行されたすべての検索のリストが含まれます。たとえば、時間のリストは次のようになります。
Time: 0 hours
-Search Terms:
-free stuff: 56
-funny pics: 321
-stackoverflow: 1234
Time: 1 hour
-Search Terms:
-ebay: 12
-funny pics: 1
-stackoverflow: 522
-BP sucks: 92
その後、1時間ごと:リストの長さが少なくとも720時間(30日間の時間数)の場合、リストの最初の要素を調べ、各検索語について、ハッシュテーブル内のその要素を適切な量だけ減らします。その後、その最初の1時間要素をリストから削除します。
721時間で、リストの最初の時間(上記)を見る準備ができたとしましょう。ハッシュテーブルの56を無料でデクリメントし、321で面白い写真をデクリメントします。その後、リスト0を完全に削除します。
高速クエリを可能にするすべての用語のソートされたリストを保持する理由は、720時間前から検索用語を調べてから1時間ごとに、上位10のリストをソートしたままにする必要があるためです。したがって、たとえばハッシュテーブルで「無料のもの」を56減らすと、リスト内の現在の場所を確認します。それは自己均衡型の二分木であるため、そのすべてはO(log(n))時間でうまく実現できます。
編集:スペースの精度を犠牲にします...
2番目のリストのように、最初のリストにも大きなリストを実装すると役立つ場合があります。次に、両方の場合に次のスペース最適化を適用できます。cronジョブを実行して、リスト内の一番上のx項目以外をすべて削除します。これにより、必要なスペースが抑えられます(その結果、リストに対するクエリが高速になります)。もちろん、おおよその結果になりますが、これは許可されています。 xは、利用可能なメモリに基づいてアプリケーションをデプロイする前に計算し、利用可能なメモリが増えたら動的に調整できます。
過去1か月の検索キーワード上位10位
密集した試行 ( tries のウィキペディアエントリから)などのメモリ効率の高いインデックス/データ構造を使用すると、メモリ要件とn-項数の関係がほぼ定義されます。
必要なメモリが利用可能な場合(仮定1)、毎月の正確な統計を保持し、毎月のすべての時間統計に集約できます。
また、「先月」を固定ウィンドウとして解釈するという前提もあります。ただし、月ごとのウィンドウがスライドしている場合でも、上記の手順は原理を示しています(スライドは、指定されたサイズの固定ウィンドウで近似できます)。
これは ラウンドロビンデータベース を思い出させますが、一部の統計は「全時間」で計算されることを除きます(すべてのデータが保持されるわけではないという意味で、rrdは平均化することで詳細を無視して期間を統合し、合計しますまたは、最大/最小値を選択すると、特定のタスクで失われる詳細は低頻度アイテムに関する情報であり、エラーが発生する可能性があります)。
仮定1
1か月間完全な統計を保持できない場合、完全な統計を保持できる特定の期間Pを見つけることができます。たとえば、ある期間Pで完全な統計があり、これが月にn回入ると仮定します。
完全な統計は、関数f(search_term) -> search_term_occuranceを定義します。
すべてのn完全な統計テーブルをメモリに保持できる場合、スライド式の月次統計は次のように計算できます。
- 最新の期間の統計を追加する
- 最も古い期間の統計を削除します(したがって、
n完全な統計テーブルを保持する必要があります)
ただし、集計レベル(月次)で上位10のみを保持する場合、一定期間の完全な統計から大量のデータを破棄できます。これにより、メモリ要件が修正された(期間Pの完全な統計テーブルの上限を想定した)作業手順が既に提供されます。
上記の手順の問題は、スライディングウィンドウの上位10語のみ(常に同様に)の情報を保持する場合、期間内にピークに達する検索語の統計情報は正しいが、時間の経過とともに常に滴り落ちる検索用語の統計。
これは、トップ10が正しいことを期待して、トップ10を超える用語、たとえばトップ100の用語に関する情報を保持することで相殺できます。
さらに分析すると、エントリが統計の一部になるために必要な最小発生回数(最大エラーに関連)を関連付けることができると思います。
(どのエントリを統計の一部とするかを決定する際に、傾向を監視および追跡することもできます。たとえば、各期間の各期間Pの発生の線形外挿が、その用語が1か月または2か月で重要になることを示している場合、既に追跡を開始している可能性があります。追跡されたプールから検索用語を削除する場合も同様の原則が適用されます。
上記の最悪のケースは、ほぼ同じ頻度の用語が多数あり、それらが常に変化する場合です(たとえば、100個の用語のみを追跡する場合、上位150個の用語が同じ頻度で発生するが、上位50個は最初の月に多く、しばらくしてから統計が正しく保持されないことがよくあります)。
また、メモリサイズが固定されていない別のアプローチが存在する可能性があります(厳密には上記のどちらでもありません)、発生/期間(日、月、年、常時)の観点で最小の重要性を定義します統計。これにより、集計中に各統計の最大エラーが保証されます(ラウンドロビンを再度参照)。
正確なソリューション
まず、正しい結果を保証するソリューションですが、大量のメモリ(大きなマップ)が必要です。
「常時」バリアント
キーとしてのクエリと値としてのカウントでハッシュマップを維持します。さらに、これまでに最も頻繁に検索されたクエリを10個、最も頻繁に検索された10番目のカウント(しきい値)のリストを保持します。
クエリのストリームが読み取られるたびにマップを常に更新します。カウントが現在のしきい値を超えるたびに、次の操作を実行します。「上位10」リストから10番目のクエリを削除し、更新したばかりのクエリに置き換えて、しきい値も更新します。
「過去1か月」のバリエーション
同じ「トップ10」リストを保持し、上記と同じ方法で更新します。また、同様のマップを保持しますが、今回は30 * 24 = 720カウント(各時間に1つ)のベクトルを値として保存します。 1時間ごとに、すべてのキーに対して次の操作を実行します。ベクトルから最も古いカウンターを削除し、最後に新しいカウンター(0に初期化)を追加します。ベクトルがすべてゼロの場合、マップからキーを削除します。また、1時間ごとに「トップ10」リストをゼロから計算する必要があります。
注:はい、今回は1つではなく720個の整数を格納していますが、キーはずっと少なくなっています(常時バリアントには実際 long tailがあります)。
近似値
これらの近似は正しいソリューションを保証するものではありませんが、メモリの消費量は少なくなります。
- N番目のクエリをすべて処理し、残りをスキップします。
- (常時バリアントのみ)マップ内に最大でM個のキーと値のペアを保持します(Mは余裕がある限り大きくする必要があります)。これは一種のLRUキャッシュです。マップにないクエリを読み込むたびに、最も使用頻度の低いクエリをカウント1で削除し、現在処理されているクエリに置き換えます。
大まかな思考...
常にトップ10
- 各用語のカウントが保存されるハッシュコレクションを使用する(用語のサニタイズなど)
- 進行中の上位10を含むソートされた配列。用語のカウントが配列内の最小カウント以上になるたびにこの配列に追加される用語/カウント
1時間ごとに更新される毎月のトップ10の場合:
- 開始モジュロ744から経過した時間数(1か月の時間数)にインデックスが付けられた配列を使用します。配列エントリは、この時間スロット中に遭遇した各用語のカウントが保存されるハッシュコレクションで構成されます。エントリは、時間スロットカウンターが変更されるたびにリセットされます
- 時間スロットでインデックス付けされたこの配列のコンテンツをコピーおよびフラット化することにより、現在の時間スロットカウンターが変更されるたびに(最大で1時間)、時間スロットでインデックス付けされた配列の統計を収集する必要があります
えっと...理にかなっていますか?私は実際の生活のようにこれを考えなかった
ああ、言及するのを忘れましたが、毎月の統計に必要な1時間ごとの「コピー/フラット化」は、すべての時間の上位10で使用された同じコードを実際に再利用できます。
"クロックページ置換アルゴリズム" (「セカンドチャンス」とも呼ばれます)の適応についてはどうですか?検索リクエストが均等に分散されていると、非常にうまく機能すると想像できます(つまり、ほとんどの検索語は5mio回ではなく定期的に表示され、二度と表示されません)。
アルゴリズムの視覚的表現は次のとおりです。 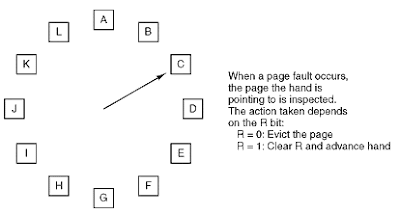
検索用語のカウントを巨大なハッシュテーブルに保存します。新しい検索では、特定の要素が1つずつ増加します。上位20程度の検索用語を追跡します。 11位の要素がインクリメントされたら、#10 *で位置を入れ替える必要があるかどうかを確認します(上位10位をソートしたままにする必要はありません。気にするのは10位と11位を区別することだけです)。
*新しい検索語が11番目にあるかどうかを確認するには、同様のチェックを行う必要があるため、このアルゴリズムは他の検索語にもバブルダウンします。そのため、少し簡略化しています。
時々、最良の答えは「わからない」です。
深く刺す。私の最初の本能は、結果をQにフィードすることです。プロセスは、Qに入ってくるアイテムを継続的に処理します。プロセスは、
期間->カウント
qアイテムが処理されるたびに、検索語を検索し、カウントをインクリメントします。
同時に、マップのトップ10エントリへの参照のリストを保持します。
現在実装されているエントリについて、そのカウントが上位10の最小エントリのカウントよりも大きいかどうかを確認します(リストにない場合)。ある場合は、最小のものをエントリに置き換えます。
それはうまくいくと思います。時間のかかる操作はありません。カウントマップのサイズを管理する方法を見つける必要があります。しかし、インタビューの回答には十分なはずです。
彼らはあなたが考えることができるかどうかを見たいと思う解決策を期待していません。その場で解決策を書く必要はありません。
Splay Tree を10ノードで使用するのはどうですか?ツリーに含まれていない値(検索語)にアクセスしようとするたびに、葉を捨て、代わりに値を挿入してアクセスします。
この背景にある考え方は、他の answer と同じです。検索用語が均等/定期的にアクセスされるという前提の下で、このソリューションは非常にうまく機能するはずです。
編集する
すぐにアクセスされる可能性のあるノードを削除しないために、ツリーに検索用語をさらに保存することもできます(他の回答で提案したソリューションでも同じです)。格納する値が多いほど、結果は良くなります。
1つの方法は、検索ごとに、その検索語とそのタイムスタンプを保存することです。そうすれば、任意の期間のトップ10を見つけることは、特定の期間内のすべての検索語を比較するだけの問題です。
アルゴリズムは単純ですが、欠点はメモリと時間の消費が大きいことです。
この問題は、一定量のメモリと「無限」(非常に大きいと考えられる)のトークンストリームがある場合に普遍的に解決できるものではありません。
大まかな説明...
理由を確認するには、入力ストリーム内のN個のトークンごとに特定のトークン(つまり、Word)Tを含むトークンストリームを検討します。
また、メモリは最大でM個のトークンへの参照(ワードIDとカウント)を保持できると仮定します。
これらの条件では、NがT間に異なるMトークンを含むほど大きい場合、トークンTが検出されない入力ストリームを構築できます。
これは、上位Nアルゴリズムの詳細とは無関係です。制限Mのみに依存します。
これが本当である理由を確認するには、2つの同一のトークンのグループで構成される着信ストリームを考えてみましょう。
T a1 a2 a3 ... a-M T b1 b2 b3 ... b-M ...
ここで、aとbはすべて、Tと等しくない有効なトークンです。
このストリームでは、a-iおよびb-iごとにTが2回表示されることに注意してください。それでも、システムからフラッシュするのに十分なことはめったにありません。
空のメモリから始めて、最初のトークン(T)がメモリ内のスロットを占有します(Mで区切られます)。その後、aがスロットを消費し、Mが使い果たされるとa-(M-1)に到達します。
A-Mが到着すると、アルゴリズムは1つのシンボルをドロップしてTにします。次のシンボルはb-1になり、a-1がフラッシュされます。
そのため、Tは、実際のカウントを構築するのに十分な時間、メモリ常駐状態を維持しません。要するに、どのアルゴリズムでも、ローカル周波数が十分に低く、グローバル周波数が高い(ストリームの長さにわたって)トークンを逃します。
ダンノ、正しく理解できたかどうか。私の解決策はヒープを使用しています。トップ10の検索項目のため、サイズ10のヒープを作成します。次に、このヒープを新しい検索で更新します。新しい検索の頻度がheap(Max Heap)topよりも大きい場合は、更新します。周波数が最小のものを放棄します。
しかし、特定の検索の頻度を計算する方法は、他の何かにカウントされます。たぶん誰もが言ったように、データストリームアルゴリズム....
Cm-sketchを使用して、開始以降のすべての検索のカウントを保存し、トップ10に対してサイズ10の最小ヒープを保持します。毎月の結果の場合、30 cm-sketch/hash-tableおよびmin-heapを保持します。過去30日、29日、..、1日からカウントおよび更新します。 1日のパスとして、最後をクリアして1日目として使用します。1時間ごとの結果についても同様に、60のハッシュテーブルと最小ヒープを保持し、最後の60、59、... 1分のカウントを開始します。分のパスとして、最後をクリアして1分として使用します。
毎月の結果は1日の範囲で正確であり、毎時の結果は1分の範囲で正確です