指定された2つのノード間のパスを見つけますか？

Question

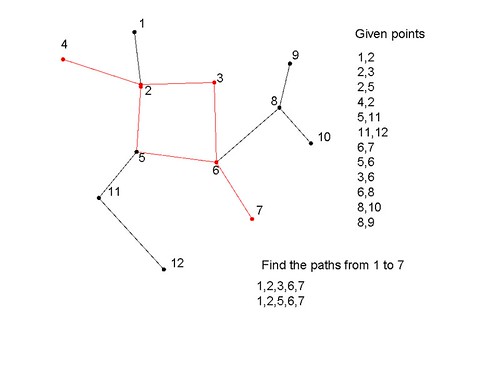
次のようにノードが接続されているとします。特定のポイント間に存在するパスの数とパスの詳細にどのように到達しますか？

1,2 //node 1 and 2 are connected 2,3 2,5 4,2 5,11 11,12 6,7 5,6 3,6 6,8 8,10 8,9

1から7までのパスを見つけます。

回答：2つのパスが見つかりました

1,2,3,6,7 1,2,5,6,7

alt text

実装が見つかりました here is Nice私は同じものを使用するつもりです

上記はPythonのリンクのスニペットです

# a sample graph graph = {'A': ['B', 'C','E'], 'B': ['A','C', 'D'], 'C': ['D'], 'D': ['C'], 'E': ['F','D'], 'F': ['C']} class MyQUEUE: # just an implementation of a queue def __init__(self): self.holder = [] def enqueue(self,val): self.holder.append(val) def dequeue(self): val = None try: val = self.holder[0] if len(self.holder) == 1: self.holder = [] else: self.holder = self.holder[1:] except: pass return val def IsEmpty(self): result = False if len(self.holder) == 0: result = True return result path_queue = MyQUEUE() # now we make a queue def BFS(graph,start,end,q): temp_path = [start] q.enqueue(temp_path) while q.IsEmpty() == False: tmp_path = q.dequeue() last_node = tmp_path[len(tmp_path)-1] print tmp_path if last_node == end: print "VALID_PATH : ",tmp_path for link_node in graph[last_node]: if link_node not in tmp_path: #new_path = [] new_path = tmp_path + [link_node] q.enqueue(new_path) BFS(graph,"A","D",path_queue) -------------results------------------- ['A'] ['A', 'B'] ['A', 'C'] ['A', 'E'] ['A', 'B', 'C'] ['A', 'B', 'D'] VALID_PATH : ['A', 'B', 'D'] ['A', 'C', 'D'] VALID_PATH : ['A', 'C', 'D'] ['A', 'E', 'F'] ['A', 'E', 'D'] VALID_PATH : ['A', 'E', 'D'] ['A', 'B', 'C', 'D'] VALID_PATH : ['A', 'B', 'C', 'D'] ['A', 'E', 'F', 'C'] ['A', 'E', 'F', 'C', 'D'] VALID_PATH : ['A', 'E', 'F', 'C', 'D']

Konrad Rudolph · Accepted Answer

幅優先検索はグラフをトラバースし、実際には開始ノードからすべてのパスを見つけます。ただし、通常、BFSはすべてのパスを保持しません。代わりに、先行機能πを更新して、最短パスを保存します。アルゴリズムを簡単に変更して、π(n)がoneの先行を保存するだけでなく、可能な先行のリストを保存することができます。

次に、すべての可能なパスがこの関数でエンコードされ、πを再帰的に走査することにより、すべての可能なパスの組み合わせを取得します。

この表記法を使用する1つの優れた擬似コードは、Cormenet al。によるIntroduction to Algorithmsで見つけることができ、その後、件名。「BFS擬似コードの前身π」をGoogleが検索して、ルートを上に Stack Exchangeでヒット。

ritesh_NITW · Answer

PYTHON expert、C++の同じコードではない人のために

//@Author :Ritesh Kumar Gupta #include <stdio.h> #include <vector> #include <algorithm> #include <vector> #include <queue> #include <iostream> using namespace std; vector<vector<int> >GRAPH(100); inline void print_path(vector<int>path) { cout<<"[ "; for(int i=0;i<path.size();++i) { cout<<path[i]<<" "; } cout<<"]"<<endl; } bool isadjacency_node_not_present_in_current_path(int node,vector<int>path) { for(int i=0;i<path.size();++i) { if(path[i]==node) return false; } return true; } int findpaths(int source ,int target ,int totalnode,int totaledge ) { vector<int>path; path.Push_back(source); queue<vector<int> >q; q.Push(path); while(!q.empty()) { path=q.front(); q.pop(); int last_nodeof_path=path[path.size()-1]; if(last_nodeof_path==target) { cout<<"The Required path is:: "; print_path(path); } else { print_path(path); } for(int i=0;i<GRAPH[last_nodeof_path].size();++i) { if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path)) { vector<int>new_path(path.begin(),path.end()); new_path.Push_back(GRAPH[last_nodeof_path][i]); q.Push(new_path); } } } return 1; } int main() { //freopen("out.txt","w",stdout); int T,N,M,u,v,source,target; scanf("%d",&T); while(T--) { printf("Enter Total Nodes & Total Edges
"); scanf("%d%d",&N,&M); for(int i=1;i<=M;++i) { scanf("%d%d",&u,&v); GRAPH[u].Push_back(v); } printf("(Source, target)
"); scanf("%d%d",&source,&target); findpaths(source,target,N,M); } //system("pause"); return 0; } /* Input:: 1 6 11 1 2 1 3 1 5 2 1 2 3 2 4 3 4 4 3 5 6 5 4 6 3 1 4 output: [ 1 ] [ 1 2 ] [ 1 3 ] [ 1 5 ] [ 1 2 3 ] The Required path is:: [ 1 2 4 ] The Required path is:: [ 1 3 4 ] [ 1 5 6 ] The Required path is:: [ 1 5 4 ] The Required path is:: [ 1 2 3 4 ] [ 1 2 4 3 ] [ 1 5 6 3 ] [ 1 5 4 3 ] The Required path is:: [ 1 5 6 3 4 ] */

Marc · Answer

ダイクストラのアルゴリズムは重み付けされたパスにより多く適用され、ポスターは最短だけでなくすべてのパスを見つけようとしているようです。

このアプリケーションの場合、グラフを作成し（アプリケーションは指示する必要がないように聞こえます）、お気に入りの検索方法を使用します。最短の推測だけでなく、すべてのパスが必要なように思えるので、選択した単純な再帰アルゴリズムを使用します。

これに関する唯一の問題は、グラフが周期的になる可能性がある場合です。

接続あり：

1、2
1、3
2、3
2、4

1-> 4からのパスを探している間、1-> 2-> 3-> 1のサイクルがあります。

その場合、ノードを走査するスタックを保持します。以下に、そのグラフのステップと結果のスタックのリストを示します（書式設定はごめんなさい-テーブルオプションはありません）：

現在のノード（可能性のある次のノードから来た場所を引いたもの）[スタック]

1（2、3）[1]
2（3、4）[1、2]
（1）[1、2、3]
1（2、3）[1、2、3、1] //エラー-スタック上の重複番号-サイクルが検出された
（）[1、2、3] //ノード3に戻り、スタックから1をポップしました。ここから探索するノードはもうありません
2（4）[1、2] //ノード2に戻り、スタックから1をポップしました。
4（）[1、2、4] //ターゲットノードが見つかりました-パスのレコードスタック。ここから探索するノードはもうありません
2（）[1、2] //ノード2に戻り、スタックから4をポップしました。ここから探索するノードはもうありません
1（3）[1] //ノード1に戻り、スタックから2をポップしました。
（2）[1、3]
2（1、4）[1、3、2]
1（2、3）[1、3、2、1] //エラー-スタック上の重複番号-サイクルが検出された
2（4）[1、3、2] //ノード2にバックステップし、スタックから1をポップしました
4（）[1、3、2、4]ターゲットノードが見つかりました-パスのレコードスタック。ここから探索するノードはもうありません
2（）[1、3、2] //ノード2にバックステップし、スタックから4ポップしました。これ以上のノード
（）[1、3] //ノード3に戻り、スタックから2をポップしました。これ以上のノード
1（）[1] //ノード1に戻り、スタックから3をポップしました。これ以上のノード
[1、2、4]と[1、3、2、4]の2つの記録されたパスで完了

Niranjan Tulpule · Answer

元のコードは少し面倒なので、BFSを使用してグラフ上の2点間にパスが存在するかどうかを調べる場合は、代わりにcollections.dequeを使用することをお勧めします。ここに私がハックした簡単な解決策があります：

注：2つのノード間にパスが存在しない場合、この方法は無限に続く可能性があります。すべてのケースをテストしたわけではありません、YMMV。

from collections import deque # a sample graph graph = {'A': ['B', 'C','E'], 'B': ['A','C', 'D'], 'C': ['D'], 'D': ['C'], 'E': ['F','D'], 'F': ['C']} def BFS(start, end): """ Method to determine if a pair of vertices are connected using BFS Args: start, end: vertices for the traversal. Returns: [start, v1, v2, ... end] """ path = [] q = deque() q.append(start) while len(q): tmp_vertex = q.popleft() if tmp_vertex not in path: path.append(tmp_vertex) if tmp_vertex == end: return path for vertex in graph[tmp_vertex]: if vertex not in path: q.append(vertex)

CapelliC · Answer

Prolog（具体的には、SWI-Prolog）

:- use_module(library(tabling)). % path(+Graph,?Source,?Target,?Path) :- table path/4. path(_,N,N,[N]). path(G,S,T,[S|Path]) :- dif(S,T), member(S-I, G), % directed graph path(G,I,T,Path).

テスト：

paths :- Graph = [ 1- 2 % node 1 and 2 are connected , 2- 3 , 2- 5 , 4- 2 , 5-11 ,11-12 , 6- 7 , 5- 6 , 3- 6 , 6- 8 , 8-10 , 8- 9 ], findall(Path, path(Graph,1,7,Path), Paths), maplist(writeln, Paths). ?- paths. [1,2,3,6,7] [1,2,5,6,7] true.

user1619876 · Answer

隣接行列が与えられた場合：

{0、1、3、4、0、0}

{0、0、2、1、2、0}

{0、1、0、3、0、0}

{0、1、1、0、0、1}

{0、0、0、0、0、6}

{0、1、0、1、0、0}

次のWolfram Mathematicaコードは問題を解決して、グラフの2つのノード間のすべての単純なパスを見つけます。単純な再帰と2つのグローバル変数を使用して、サイクルを追跡し、目的の出力を保存しました。コードは、コードを明確にするためだけに最適化されていません。「印刷」は、それがどのように機能するかを明確にするのに役立つはずです。

cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True]; getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]]; builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos}, If[{node} != {} && node != endNode , root = node; nodes = getNode[matrix, node]; (*Print["root:",root,"---nodes:",nodes];*) AppendTo[lcycle, Flatten[{root, nodes}]]; If[cycleQ[lcycle] == True, lcycle = Most[lcycle]; appendToTree[root, nodes];, Print["paths: ", tree, "
", "root:", root, "---nodes:",nodes]; appendToTree[root, nodes]; ]; ]; appendToTree[root_, nodes_] := Block[{pos, toAdd}, pos = Flatten[Position[tree[[All, -1]], root]]; For[i = 1, i <= Length[pos], i++, toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes; (* check cycles!*) If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd; ]; tree = Delete[tree, {#} & /@ pos]; builtTree[#, matrix] & /@ Union[tree[[All, -1]]]; ]; ];

コードを呼び出すには：initNode = 1; endNode = 6; lcycle = {};ツリー= {{initNode}}; builtTree [initNode、matrix];

パス：{{1}}ルート：1 ---ノード：{2,3,4}

パス：{{1,2}、{1,3}、{1,4}}ルート：2 ---ノード：{3,4,5}

パス：{{1,3}、{1,4}、{1,2,3}、{1,2,4}、{1,2,5}}ルート：3 ---ノード：{2、 4}

パス：{{1,4}、{1,2,4}、{1,2,5}、{1,3,4}、{1,2,3,4}、{1,3,2、 4}、{1,3,2,5}}ルート：4 ---ノード：{2,3,6}

パス：{{1,2,5}、{1,3,2,5}、{1,4,6}、{1,2,4,6}、{1,3,4,6}、{ 1,2,3,4,6}、{1,3,2,4,6}、{1,4,2,5}、{1,3,4,2,5}、{1,4、 3,2,5}}ルート：5 ---ノード：{6}

結果：{{1、4、6}、{1、2、4、6}、{1、2、5、6}、{1、3、4、6}、{1、2、3、4、 6}、{1、3、2、4、6}、{1、3、2、5、6}、{1、4、2、5、6}、{1、3、4、2、5 6}、{1、4、3、2、5、6}}

...残念ながら、より良い方法で結果を表示するために画像をアップロードすることはできません:(

http://textanddatamining.blogspot.com

v3. · Answer

すべてのパスが必要な場合は、再帰を使用します。

隣接リストを使用して、できれば、訪問済み頂点の現在のリストを埋めようとする関数f()）を作成してください。

void allPaths(vector<int> previous, int current, int destination) { previous.Push_back(current); if (current == destination) //output all elements of previous, and return for (int i = 0; i < neighbors[current].size(); i++) allPaths(previous, neighbors[current][i], destination); } int main() { //...input allPaths(vector<int>(), start, end); }

ベクトルは値で渡されるため（したがって、再帰的手順でさらに下に行われた変更は永続的ではありません）、すべての可能な組み合わせが列挙されます。

previous vectorを参照渡しすることで少し効率を上げることができます（したがって、ベクトルを何度もコピーする必要はありません）が、手動でpopped_back（）を取得する必要があります。

もう1つ：グラフにサイクルがある場合、これは機能しません。（この場合、すべてのsimpleパスを見つけたいと思います）previousベクトルに何かを追加する前に、まずそれが既にあるかどうかを確認します。

すべての最短パスが必要な場合は、このアルゴリズムでKonradの提案を使用してください。