web-dev-qa-db-ja.com

自然数nに対してn個の異なる色を生成する方法は？

N = 100と言います。視覚的に区別できる100色を生成するにはどうすればよいですか？これは数学的に可能ですか？

algorithmcolorspseudocodeperception
38
deostroll

100は多くの色ですが、HSBまたはHSL空間で可能な限りまばらにそれらを分散することによってそれを行うことができる場合があります。 RGBで行うのはおそらく難しいでしょう。

たとえば、10の異なる色相、4つの異なる彩度レベル、3つの異なる明るさ設定を使用すると、最大120色を使用できます。彩度と明度の値を慎重に選択する必要があります。人間の目は複雑で紛らわしいセンサーです。色空間を円錐として扱う場合、おそらく各明度/彩度レベルで異なる数の色相が必要になります。

これがウィキペディアへのリンクです HSBのエントリ 。

6
Carl Norum

うん。明確に定義することは、色空間に延期することの結果であり、最大限に明確な色を言うとき、私たちが言う意味は、他のすべての色から可能な限り遠い色です。しかし、色空間は変化しないので、答えは変化しません。また、人間の目により適したものを実装し、人間の目がCIE-lab de2000の色距離のように色をどのように見るかを実装すると、すべての計算をやり直すことが難しくなりますが、静的なリストは簡単になります。 128のエントリがあります。

private static final String[] indexcolors = new String[]{
        "#000000", "#FFFF00", "#1CE6FF", "#FF34FF", "#FF4A46", "#008941", "#006FA6", "#A30059",
        "#FFDBE5", "#7A4900", "#0000A6", "#63FFAC", "#B79762", "#004D43", "#8FB0FF", "#997D87",
        "#5A0007", "#809693", "#FEFFE6", "#1B4400", "#4FC601", "#3B5DFF", "#4A3B53", "#FF2F80",
        "#61615A", "#BA0900", "#6B7900", "#00C2A0", "#FFAA92", "#FF90C9", "#B903AA", "#D16100",
        "#DDEFFF", "#000035", "#7B4F4B", "#A1C299", "#300018", "#0AA6D8", "#013349", "#00846F",
        "#372101", "#FFB500", "#C2FFED", "#A079BF", "#CC0744", "#C0B9B2", "#C2FF99", "#001E09",
        "#00489C", "#6F0062", "#0CBD66", "#EEC3FF", "#456D75", "#B77B68", "#7A87A1", "#788D66",
        "#885578", "#FAD09F", "#FF8A9A", "#D157A0", "#BEC459", "#456648", "#0086ED", "#886F4C",

        "#34362D", "#B4A8BD", "#00A6AA", "#452C2C", "#636375", "#A3C8C9", "#FF913F", "#938A81",
        "#575329", "#00FECF", "#B05B6F", "#8CD0FF", "#3B9700", "#04F757", "#C8A1A1", "#1E6E00",
        "#7900D7", "#A77500", "#6367A9", "#A05837", "#6B002C", "#772600", "#D790FF", "#9B9700",
        "#549E79", "#FFF69F", "#201625", "#72418F", "#BC23FF", "#99ADC0", "#3A2465", "#922329",
        "#5B4534", "#FDE8DC", "#404E55", "#0089A3", "#CB7E98", "#A4E804", "#324E72", "#6A3A4C",
        "#83AB58", "#001C1E", "#D1F7CE", "#004B28", "#C8D0F6", "#A3A489", "#806C66", "#222800",
        "#BF5650", "#E83000", "#66796D", "#DA007C", "#FF1A59", "#8ADBB4", "#1E0200", "#5B4E51",
        "#C895C5", "#320033", "#FF6832", "#66E1D3", "#CFCDAC", "#D0AC94", "#7ED379", "#012C58"
};

これが画像としての最初の256です。

max distance

（左から右）（上から下）。各色が色空間内で可能な限り等距離にあることを確認すると、さらにいくつかの異なる色を取得できる場合があります。そのルックアップテーブルは、最初にNを指定して色空間をマッピングするのではなく、追加の各色を以前のすべての色と最大限に区別するものとして選択します。ええ、ブルートフォースと高レベルのカラーダンスアルゴリズムで、これと同じ色のセットを自分で作成する準備が整いました。 1日かそこら。

42
Tatarize

編集：

私はこの分野の専門知識がなく、私の数学のスキルはかなり平均的です。しかし、私はこの問題の解決策がここでの多くの回答が示唆するよりも複雑で興味深いものであると私は考えています。私が最近同様のことを試みたが解決策が見つからなかったからです。

色の違い

色の知覚はもちろん主観的ですが、人間の間には重要な合意があります。たとえば、赤、緑、青は非常に異なる色であり、色覚異常の人でも黒と白は非常に異なると同意することができます。

RGB

コンピュータシステムにおける最も一般的な色の表現は、ベクトル（r、g、b）です。これは、次のような単純な距離関数を示唆しています。

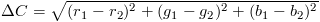
RGB color difference

r、g、bの範囲を[0、1]そしてこれがどのように機能するかを見てください：

  1. 赤（1、0、0）と赤（1、0、0）の距離は、それは明白であるはずです
  2. 赤（1、0、0）と黄色（1、1、0）の距離は1、これは距離よりも小さい
  3. 赤（1、0、0）と青（0、0、1）はsqrt（2）、もっともらしい

ここまでは順調ですね。ただし、問題は、青と赤の距離が黒1から黒（0、0、0）、しかし、画像を見ると、これは当てはまらないようです：

blue and red on black

また、黄色（1、1、0）とマゼンタ（1、0、1）は両方とも同じ距離1from white（1、1、1）、これはどちらにも意味がないようです：

yellow and Magenta on white

HSLおよびHSV

HSLとHSVの配色 のアナログメトリックには同じ問題があると仮定しても安全だと思います。これらの配色は、色を比較するためのものではありません。

CIEDE2000

幸いなことに、すでに色を比較するための良い方法を見つけようとしている科学者がいます。彼らはいくつかの精巧な方法を考え出しました、最新のものは CIEDE20 です

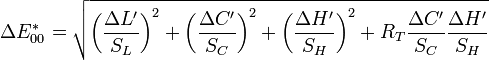
CIEDE2000

（記事に記載されている完全な式はhugeです）

この測定基準は、人間の知覚を考慮に入れています。たとえば、青の色合いを十分に識別できないように見えるという事実です。したがって、これを色差関数として使用します。

カラーピッキングアルゴリズム

素朴なソリューション

いくつかの回答は次のアルゴリズムを提案しました

colors = []
for n in range(n):
    success=False
    while not success:
        new_color = random_color()
        for color in colors:
            if distance(color, new_color)>far_enough:
                colors.append(new_color)
                success = True
                break

このアルゴリズムにはいくつかの問題があります：

  1. 色の間隔が最適ではありません。色が線上の数値のようであると想像すると、3つの数値は次のように最適な間隔で配置されます。

    | a ----- b ----- c |

    A、b、cを移動せずにさらに1つの数値をパックすることは、すべての色を再調整するよりも明らかに悪いです。

  2. アルゴリズムの終了は保証されていません。リストの既存の色から十分な色がない場合はどうなりますか？ループは永遠に続きます

適切なソリューション

ええと..持っていません。

37
Otto Allmendinger

HSLに変換してから、他の2つの値を一定に保ちながら、色相（H）の値を反復処理します。

値ごとに HSLからRGBに変換 。

私の回答 ここ および ここ を参照してください。

Nが非常に大きく、したがって色が視覚的に区別できない場合は、その時点で同じ色相すべてについて繰り返し、他のコンポーネントを変更して彩度または明度を変えることができます。したがって、基本的には使用する色相値の最大数を設定することができ、一度ヒットすると、異なる彩度または明度でやり直すことができます。

4
Brian R. Bondy

あなたの質問に対する答えではありませんが、nに最大値があり、アプリケーションがそれを許可している場合、次のような定義済みの色のリストを使用できます。

http://en.wikipedia.org/wiki/List_of_colors

1つの利点は、色覚異常の人のためにツールチップに人間が読める色名を表示できることです。

2
Carlos Gutiérrez

まず、RGBスペースを使用しないでください。この問題のために悪い色空間を見つけるのは難しいです。 （表示用または印刷用のどちらの色を使用しているかに応じて、黒に近いか白に近い、区別できない膨大な数の色があります。）

ラボスペースを使用する場合、色の視覚的な近さを測定するための知覚的カラーモデル（CIE 1996？およびCIE 2000）があります（それぞれ印刷と表示用）。

色を一度計算して結果を保存するのか、それともその場で再計算する必要があるのか​​（そしてその場合、確定的である必要があるかどうか）はわかりません。明らかに、セットを生成するための最良の方法についての議論は、それに依存します。

ただし、カラースペースの軸を均等に分割し（たとえば、8に分割）、それらを初期点として使用すると、ランダムプロセスよりもはるかに効率的であることをお勧めします。確かに、任意の点をその近傍と比較するだけで済みます（それらがすでにセットにある場合に限られます）。これにより、膨大な数の比較を節約できます。

1
user280592