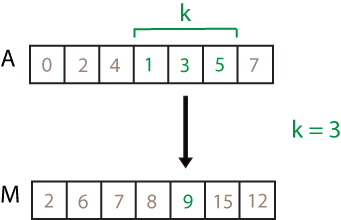
合計が範囲内にあるトリプレット（1,2）

Question

配列のn正の実数を指定して、このセットの中にトリプレットが存在するかどうかを調べます。範囲内 (1, 2)。線形時間と一定の空間でそれを行います。

配列は順序付けされていません。

数値は正です

数値は実数

どんな助けでも大歓迎です。ありがとう。

Soul Ec · Accepted Answer

秘訣は、可能な解決策を分類し、それぞれについて線形時間の一定空間の解決策を考え出す方法を理解することです。

3つの範囲X = (0,2/3), Y = [2/3,1], Z = (1,2)を考えます。最大で1つの値はZから取得できます（2つの値がZから取得された場合、合計は_1+1=2_を超えます）。同様に、少なくとも1つの値はXから取得する必要があります。 _a <= b <= c_となるように、3つの値_1 <= a+b+c <= 2_があったとします。次に、どのような可能なクラスのソリューションが実行可能かを検討します。

_A) `a \in X, b \in X, C \in X` B) `a \in X, b \in X, C \in Y` C) `a \in X, b \in X, C \in Z` D) `a \in X, b \in Y, C \in Y` E) `a \in X, b \in Y, C \in Z` _

それでは、各ケースをどのようにテストできますか？

ケースAは非常に簡単にテストできます。合計が2未満であることが保証されているため、最大合計（Xの最大3要素）が1を超えることをテストするだけで済みます。

ケースCは非常に簡単にテストできます。合計が1を超えることが保証されているため、合計が2未満かどうかを確認するだけで済みます。そのためには、Xの最小2つの値とZの最小値

ケースDとEはCに似ています（合計は少なくとも4/3> 1でなければならないため、各クラスで可能な最小の値を選択してください）。

ケースBが唯一のトリッキーなケースです。 _0 < a+b < 4/3_および_2/3 <= c <= 1_。ケースBを処理するために、X1 =（0、1/2）、X2 = [1/2 2/3）、Y = [2/3、1]の間隔を考慮します。

これにより、次の3つの有効なケースが発生します。

B1。 X1のa、X2のb、Yのc

B2。 X1のa、X1のb、Yのc

B3。 X2のa、X2のb、Yのc

ケースB1およびB3：3つの数値の合計は常に1より大きいため、最小値を取り、2より小さいかどうかを確認します。

ケースB2：3つの数値の合計が常に2未満であるため、最大合計を取り、1より大きいかどうかを確認します。

要約すると、テストは次のとおりです。

_|X| >= 3_およびXmax(1) + Xmax(2) + Xmax(3) >= 1
_|X| >= 2_、_|Z| >= 1_、およびXmin(1)+Xmin(2)+Zmin(1) <= 2
_|X| >= 1_、_|Y| >= 2_、およびXmin(1)+Ymin(1)+Ymin(2) <= 2
_|X| >= 1_、_|Y| >= 1_、_|Z| >= 1_、およびXmin(1)+Ymin(1)+Zmin(1) <= 2
_|X| >= 2_、_|Y| >= 1_、およびXmax(1) + Xmax(2) + Ymin(1) < 2
_|X| >= 2_、_|Y| >= 1_、およびXmin(1) + Xmin(2) + Ymax(1) > 1）

各テストは線形時間と一定の空間で実行できます（Xmax(1), Xmax(2), Xmax(3), Xmin(1), Xmin(2), Ymin(1), Ymin(2), Ymax(1), Zmin(1)を見つけるだけで済み、データが並べ替えられていなくても、すべて1回のパスで見つけることができます）

Prince Raj · Answer

したがって、長さnのdoubleデータ型の配列があります。 3つの変数a、b、cを配列の最初の3つの値として初期化します。次に、i = 3からnまで反復し、以下を確認します。1）合計が（1、2）にあるかどうかを確認します。 2）そうでない場合は、合計が2より大きいかどうかを確認します。そうであれば、MAX（a、b、c）を現在の要素arr [i]に置き換えます。 3）それ以外の場合、合計は1未満でなければならず、次にMIN（a、b、c）を現在の要素arr [i]に置き換えます。最後に、ループから出た後、合計が（1,2）に入る場合、最後のトリプレットについてもう一度チェックします。 trueを返すか、そうでなければfalseを返します。

enter code here double a=arr[0], b=arr[1], c=arr[2]; for(int i=3 ; i<n ; i++){ // check if sum fall in (1, 2) if(a+b+c > 1 && a+b+c < 2){ return 1; } // if not, then check is sum greater than 2 // if so, then replece MAX(a,b,c) to new number else if(a+b+c > 2){ if(a>b && a>c){ a = arr[i]; } else if(b>a && b>c){ b = arr[i]; } else if(c>a && c>b){ c = arr[i]; } } // else then sum must be less than 1 // then replace MIN(a,b,c) to new number else{ if(a<b && a<c){ a = arr[i]; } else if(b<a && b<c){ b = arr[i]; } else if(c<a && c<b){ c = arr[i]; } } } // check for last a, b, c triplet if(a+b+c > 1 && a+b+c < 2){ return 1; } else{ return 0; }

Amitrajit Bose · Answer

この問題は、スライディングウィンドウ合計アプローチを使用して、線形ランタイム時間で簡単に解決できます。この場合、サイズ3のウィンドウを使用します。これは、「移動合計アルゴリズム」とも呼ばれます。

以下のアルゴリズム

1> Prepare the window of size 3 with the first 3 elements 2> IF (array.len <= 3): CHECK IF window-sum is in the range (1,2), then RETURN accordingly 3> FOR i = 3 UPTO (array.len-1) 3.1> SORT the window (3log3 = constant time operation) 3.2> IF window-sum is in the range (1,2): RETURN 1 or TRUE 3.3> ELSE IF window-sum < 1: Replace the smallest element in the window (window[0]) with array[i] 3.4> ELSE IF window-sum > 2: Replace the largest element in the window (window[2]) with array[i] 4> Outside the loop, check the FINAL window sum and RETURN accordingly.

Pythonコードはこちらにアクセスしてください。リポジトリにスターを付けてください！

mrinali mangal · Answer

ソリューションはc ++にあります（interviewbbitソリューション）

int Solution::solve(vector<string> &arr) { int n=arr.size(),i; vector<float>v; for(i=0;i<n;i++) { v.Push_back(stof(arr[i])); } float a=v[0],b=v[1],c=v[2]; float mx=0; for(i=3;i<n;i++) { if(a+b+c<2 && a+b+c>1) return 1; else if(a+b+c>2) { if(a>b && a>c) a=v[i]; else if(b>a && b>c) b=v[i]; else c=v[i]; } else { if(a<b && a<c) a=v[i]; else if(b<a && b<c) b=v[i]; else c=v[i]; } } if(a+b+c>1 && a+b+c<2) return 1; else return 0; }

Manish Sakariya · Answer

@soul Ecによって与えられたソリューションのJavaコード。

ケースBを変更する必要があります。数値がa + b + cであるとします。

there are three ranges x1 x2 y (0,1/2) (1/2,2/3) (2/3,1)

we have 4 possibilities 1. x1 + x1 +y 2. x2 + x2 +y 3. x1 + x2 +y 4 x2 + x1 +y

ここでは、ケース3と4は同じです。したがって、3つのケースのみがあります。

1. x1 + x1 + y it is always <2 ( do x1max+x1max+ymax <2 to verify) so we have to check if x1max(1)+x1max(2)+ymax(1) > 1 2. x2 + x2 + y it is always >1 ( do x2min+x2min+ymin >1 to verify) so we have to check if x2min(1)+x2min(2)+ymin(1) <=2 3. x1 + x2 + y it is always >1 (do x1min+x2min+ymin >1 to verify) so we have to check if x1min(1)+x2min(1)+ymin(1)<=2

 public static int solve(ArrayList<String> A) { double d[]= new double[A.size()]; for(int i=0;i<A.size();i++) { d[i]= Double.parseDouble(A.get(i)); } double range1 = 0; double range2 = (double) 2/3; double range3 = 1; double range4 = 2; double range02 =(double) 1/2; // min and max in range (0,2/3) double min1= Double.MAX_VALUE; double min2=Double.MAX_VALUE; double min3=Double.MAX_VALUE; double max1= Double.MIN_VALUE; double max2=Double.MIN_VALUE; double max3=Double.MIN_VALUE; // min and max in range (2/3,1) double miny1= Double.MAX_VALUE; double miny2=Double.MAX_VALUE; double miny3=Double.MAX_VALUE; double maxy1= Double.MIN_VALUE; double maxy2=Double.MIN_VALUE; double maxy3=Double.MIN_VALUE; // min and max in range (1,2) double minz1= Double.MAX_VALUE; double minz2=Double.MAX_VALUE; double minz3=Double.MAX_VALUE; double maxz1= Double.MIN_VALUE; double maxz2=Double.MIN_VALUE; double maxz3=Double.MIN_VALUE; // min and max in range (0,1/2) double minxx1= Double.MAX_VALUE; double minxx2=Double.MAX_VALUE; double minxx3=Double.MAX_VALUE; double maxx1= Double.MIN_VALUE; double maxx2=Double.MIN_VALUE; double maxx3=Double.MIN_VALUE; // min and max in range (1/2,2/3) double minyy1= Double.MAX_VALUE; double minyy2=Double.MAX_VALUE; double minyy3=Double.MAX_VALUE; double maxyy1= Double.MIN_VALUE; double maxyy2=Double.MIN_VALUE; double maxyy3=Double.MIN_VALUE; for (int i = 0; i < d.length; i++) { if (d[i] >= range1 && d[i] < range02) { if (d[i] < minxx3) { minxx1=minxx2; minxx2=minxx3; minxx3 = d[i]; } else if (d[i] > minxx3 && d[i] < minxx2) { minxx1=minxx2; minxx2 = d[i]; } else if (d[i] > minxx3 && d[i] > minxx2 && d[i] < minxx1) { minxx1 = d[i]; } if (d[i] > maxx3) { maxx1=maxx2; maxx2=maxx3; maxx3 = d[i]; } else if (d[i] < maxx3 && d[i] > maxx2) { maxx1=maxx2; maxx2 = d[i]; } else if (d[i] < maxx3 && d[i] < maxx2 && d[i] > maxx1) { maxx1 = d[i]; } } if (d[i] >= range02 && d[i] < range2) { if (d[i] < minyy3) { minyy1=minyy2; minyy2=minyy3; minyy3 = d[i]; } else if (d[i] > minyy3 && d[i] < minyy2) { minyy1=minyy2; minyy2 = d[i]; } else if (d[i] > minyy3 && d[i] > minyy2 && d[i] < minyy1) { minyy1 = d[i]; } if (d[i] > maxyy3) { maxyy1=maxyy2; maxyy2=maxyy3; maxyy3 = d[i]; } else if (d[i] < maxyy3 && d[i] > maxyy2) { maxyy1=maxyy2; maxyy2 = d[i]; } else if (d[i] < maxyy3 && d[i] < maxyy2 && d[i] > maxyy1) { maxyy1 = d[i]; } } if (d[i] >= range1 && d[i] < range2) { if (d[i] < min3) { min1=min2; min2=min3; min3 = d[i]; } else if (d[i] > min3 && d[i] < min2) { min1=min2; min2 = d[i]; } else if (d[i] > min3 && d[i] > min2 && d[i] < min1) { min1 = d[i]; } if (d[i] > max3) { max1=max2; max2=max3; max3 = d[i]; } else if (d[i] < max3 && d[i] > max2) { max1=max2; max2 = d[i]; } else if (d[i] < max3 && d[i] < max2 && d[i] > max1) { max1 = d[i]; } } if (d[i] >= range2 && d[i] < range3) { if (d[i] < miny3) { miny1=miny2; miny2=miny3; miny3 = d[i]; } else if (d[i] > miny3 && d[i] < miny2) { miny1=miny2; miny2 = d[i]; } else if (d[i] > miny3 && d[i] > miny2 && d[i] < miny1) { miny1 = d[i]; } if (d[i] > maxy3) { maxy1=maxy2; maxy2=maxy3; maxy3 = d[i]; } else if (d[i] < maxy3 && d[i] > maxy2) { maxy1=maxy2; maxy2 = d[i]; } else if (d[i] < maxy3 && d[i] < maxy2 && d[i] > maxy1) { maxy1 = d[i]; } } if (d[i] >= range3 && d[i] <= range4) { if (d[i] < minz3) { minz1=minz2; minz2=minz3; minz3 = d[i]; } else if (d[i] > minz3 && d[i] < minz2) { minz1=minz2; minz2 = d[i]; } else if (d[i] > minz3 && d[i] > minz2 && d[i] < minz1) { minz1 = d[i]; } if (d[i] > maxz3) { maxz1=maxz2; maxz2=maxz3; maxz3 = d[i]; } else if (d[i] < maxz3 && d[i] > maxz2) { maxz1=maxz2; maxz2 = d[i]; } else if (d[i] < maxz3 && d[i] < maxz2 && d[i] > maxz1) { maxz1 = d[i]; } } } if(max1+max2+max3>=1 && max1!=Double.MIN_VALUE && max2!=Double.MIN_VALUE && max3!=Double.MIN_VALUE) return 1; if(min3+min2+minz3<=2 && min3!=Double.MAX_VALUE && min2!=Double.MAX_VALUE && minz3!=Double.MAX_VALUE ) return 1; if(min3+miny3+miny2<=2 && min3!=Double.MAX_VALUE && miny3!=Double.MAX_VALUE && miny2!=Double.MAX_VALUE) return 1; if(min3+miny3+minz3<=2 && min3!=Double.MAX_VALUE && miny3!=Double.MAX_VALUE && minz3!=Double.MAX_VALUE) return 1; if(maxx3+maxx2+maxy3>1 && maxx3!=Double.MIN_VALUE && maxx2!=Double.MIN_VALUE && maxy3!=Double.MIN_VALUE) { return 1; } if(minyy3+minyy2+miny3<=2 && minyy3!=Double.MAX_VALUE && minyy2!=Double.MAX_VALUE && miny3!=Double.MAX_VALUE) { return 1; } if(minxx3+minyy3+miny3<=2 && minxx3!=Double.MAX_VALUE && minyy3!=Double.MAX_VALUE && miny3!=Double.MAX_VALUE) { return 1; } return 0; }

SaCh · Answer

@Soul Ecのアイデアを基に、これが私が思いついたコードです。完全に問題なく動作します。

vector<double> x; vector<double> y; vector<double> z; double d = (double)2/3; for(i = 0 ; i < arr.size() ; i++){ if(arr[i] >= 0 && arr[i] < d) x.Push_back(arr[i]); else if(arr[i] >= d && arr[i] <= 1) y.Push_back(arr[i]); else z.Push_back(arr[i]); } sort(x.begin(), x.end()); sort(y.begin(), y.end()); sort(z.begin(), z.end()); int xsz = x.size(); int ysz = y.size(); int zsz = z.size(); if(xsz >= 3 && x[xsz-1] + x[xsz-2] + x[xsz-3] >= 1.0) return 1; if(xsz >= 2 && zsz >= 1 && x[0] + x[1] + z[0] <= 2.0) return 1; if(xsz >= 1 && ysz >= 2 && x[0] + y[0] + y[1] <= (double)2.0) return 1; if(xsz >= 1 && ysz >= 1 && zsz >= 1 && x[0] + y[0] + z[0] <= 2.0) return 1; if(xsz >= 2 && ysz >= 1){ if(x[xsz-1] + x[xsz-2] + y[0] < 2.0 && x[xsz-1] + x[xsz-2] + y[0] > 1.0) return 1; if(x[0] + x[1] + y[ysz-1] > 1.0 && x[0] + x[1] + y[ysz-1] < 2.0) return 1; }