数値がフィボナッチかどうかをテストします
私はフィボナッチ数のリストを作成する方法を知っていますが、特定の数がフィボナッチリストに属しているかどうかをテストする方法はわかりません-念頭に置く方法の1つはfibのリストを生成することです。その番号までの番号とそれが配列に属しているかどうかを確認しますが、別のより簡単で高速な方法が必要です。
何か案は ?
非常に良いテストは、5 N^2 + 4または5N^2 – 4が平方数である場合にのみ、Nがフィボナッチ数であることです。数値が正方形であることを効率的にテストする方法のアイデアについては、 SOの説明 を参照してください。
お役に立てれば
#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
echo "$victim is a fibonacci number"
else
echo "$victim aint"
fi
数字のサイズが制限されている場合、上限より下のすべてのフィボナッチ数をハッシュテーブルに入れて、包含をテストするだけでうまくいきます。フィボナッチ数は指数関数的に増加するため、ごくわずかです(たとえば、5mlnの下の38個のみ)。
数値が制限サイズのnotである場合、平方テストで推奨されるトリックは、数値が見つかるかそれを超えるまでフィボナッチ数列を生成するよりもほぼ確実に遅くなります。
ソリューションに向けて、Binetのフォーミュラをご覧ください。
(ウィキペディアの フィボナッチ数 の下にある「閉形式表現」を探してください)
フィボナッチ数列は単純な閉じた式によって作成されると言っています:
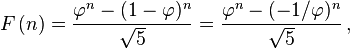
nを解いて、nが整数かどうかをテストすると、答えが得られると思います。
Edit@psmearsが指摘しているように、同じウィキペディアの記事にもフィボナッチ数の検出に関するセクションがあります。ウィキペディアは優れた情報源です。
正の整数ωはフィボナッチ数
1つの5ωの場合にのみ2 + 4および5ω2 -4は完全な正方形です
fromAlfred PosamentierとIngmar Lehmannによる(すばらしい)FIBONACCI番号
bool isFibonacci(int w)
{
double X1 = 5 * Math.Pow(w, 2) + 4;
double X2 = 5 * Math.Pow(w, 2) - 4;
long X1_sqrt = (long)Math.Sqrt(X1);
long X2_sqrt = (long)Math.Sqrt(X2);
return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}
1kと10kの間のフィボナッチ数を出力するスニペット。
for (int i = 1000; i < 10000; i++)
{
if (isFibonacci(i))
Console.Write(" "+i);
}
OMG 4つしかありません!!!
他の方法で
from math import *
phi = 1.61803399
sqrt5 = sqrt(5)
def F(n):
return int((phi**n - (1-phi)**n) /sqrt5)
def isFibonacci(z):
return F(int(floor(log(sqrt5*z,phi)+0.5))) == z
print [i for i in range(1000,10000) if isFibonacci(i)]
フィボナッチ数に関するウィキペディアの記事 のセクション「フィボナッチ数の認識」を参照してください。
フィボナッチ数は指数関数的に増加するため、提案する方法は非常に高速です。もう1つは this です。
私とpsmearsによる以前の回答に基づいて、このC#コードを作成しました。
それはゆっくりとステップを通過し、明らかに削減および最適化できます。
// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
// eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
double root5 = Math.Sqrt(5);
double PSI = (1 + root5) / 2;
// For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number
double a;
a = T*root5;
a = Math.Log(a) / Math.Log(PSI);
a += 0.5;
a = Math.Floor(a);
idx = (Int32)a;
long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);
if (u == T)
{
return true;
}
else
{
idx = 0;
return false;
}
}
テストでは、これが最初の69個のフィボナッチ数で機能することが明らかになりましたが、70個目では故障します。
F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails
全体として、何らかのBigIntライブラリを使用している場合を除き、フィボナッチ数の単純なルックアップテーブルを作成し、アルゴリズムを実行するよりもそれを確認する方がおそらく良いでしょう。
最初の300個の番号のリストは、オンラインで簡単に入手できます。
ただし、十分な精度があり、数値表現システムがオーバーフローしない限り、このコードは実行可能なアルゴリズムの概要を示しています。
Re:Ahmadのコード-再帰やポインターを使用しない単純なアプローチで、かなり単純ですが、実際のタイタニック数に満たないものにはほとんど計算能力を必要としません最悪の場合)
//見つかった場合はposを返し、見つからない場合は0を返します(C/C++は値!= 0をtrueとして扱うため、同じ結果になります)
int isFib (long n)
{
int pos = 2;
long last = 1;
long current = 1;
long temp;
while (current < n)
{
temp = last;
last = current;
current = current + temp;
pos++;
}
if (current == n)
return pos;
else
return 0;
}
ウィキペディアから: http://en.wikipedia.org/wiki/Fibonacci_number
正の整数zは、5z ^ 2 + 4または5z ^ 2 − 4のいずれかが完全な正方形である場合にのみ、フィボナッチ数です。
フィボナッチ数の一般的な式はF(n) = [[(1 + sqrt(5))/ 2] sup n + 1-[(1-sqrt(5)))/ 2] sup n + 1]/sqrt(5).....(*)2番目の指数関数は、nが大きく、数値演算を実行すると0になりますF(n) = [(1.618)sup n + 1]/2.236
Kがテストされる数である場合、log(k * 2.2336)/ log(1.618)は整数でなければなりません!
Kが13の例では、計算機は7.00246を返します。Kが14の場合、答えは7.1564です。
回答に最も近い整数を取得し、(*)を代入して結果がKであることを確認することで、結果の信頼性を高めることができます。
ここで紹介したメソッドのベンチマークをいくつか実行し、単純な追加、配列の事前計算、結果のハッシュ化を行いました。少なくともPerlの場合、二乗法は対数法よりも少し速く、おそらく20%高速です。 abelenkyが指摘しているように、ビット数を二乗する余地があるかどうかはトレードオフです。
確かに、最も速い方法は、ドメイン空間のすべてのフィボナッチ数をハッシュすることです。 abelenkyが作成する別のポイントの線に沿って、2 ^ 64未満のこれらの吸盤は94個しかありません。
それらを事前に計算して、Perlハッシュ、Python辞書、またはその他のものに入れてください。
フィボナッチ数のプロパティは非常に興味深いですが、コンピュータプログラムの整数が1であるかどうかを判断するために使用することは、プログラムを起動するたびにpiを計算するサブルーチンを記述するようなものです。
これは私のソリューションであり、ベンチマークかどうかはわかりません。これがお役に立てば幸いです!
def is_fibonacci?(i)
a,b=0,1
until b >= i
a,b=b,a+b
return true if b == i
end
end
a、b = b、a + bは何をしていますか
0, 1 = 1, 0 +1
1, 1 = 1, 1 + 1
1, 2 = 2, 1 + 2
2, 3 = 3, 2 + 3
fib1 = fib2
fib2 = fib1 + fib2
A Scala version-
def isFib(n: Int): Boolean = {
def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {
if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)
}
checkFib()
}
扱っている数字はどれくらいですか?
ルックアップテーブルはあなたのために働くことができますか? (検索可能な番号の事前計算済みリスト)
閉じた形の式 もあり、分析的に答えを得るために反転することができると思います(数学者ではないので、この提案が理にかなっているとは約束できません)
Javaソリューションは次のように実行できます。しかし、それでも最適化できます
次の解決策は
- 1≤T≤10^ 5
- 1≤N≤10^ 10
Tはテストケースの数、Nは数の範囲
import Java.util.Scanner;
import Java.math.BigDecimal;
import Java.math.RoundingMode;
public class FibonacciTester {
private static BigDecimal zero = BigDecimal.valueOf(0);
private static BigDecimal one = BigDecimal.valueOf(1);
private static BigDecimal two = BigDecimal.valueOf(2);
private static BigDecimal four = BigDecimal.valueOf(4);
private static BigDecimal five = BigDecimal.valueOf(5);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
BigDecimal[] inputs = new BigDecimal[n];
for (int i = 0; i < n; i++) {
inputs[i] = sc.nextBigDecimal();
}
for (int i = 0; i < inputs.length; i++) {
if (isFibonacci(inputs[i]))
System.out.println("IsFibo");
else
System.out.println("IsNotFibo");
}
}
public static boolean isFibonacci(BigDecimal num) {
if (num.compareTo(zero) <= 0) {
return false;
}
BigDecimal base = num.multiply(num).multiply(five);
BigDecimal possibility1 = base.add(four);
BigDecimal possibility2 = base.subtract(four);
return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
}
public static boolean isPerfectSquare(BigDecimal num) {
BigDecimal squareRoot = one;
BigDecimal square = one;
BigDecimal i = one;
BigDecimal newSquareRoot;
int comparison = -1;
while (comparison != 0) {
if (comparison < 0) {
i = i.multiply(two);
newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
} else {
i = i.divide(two);
newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
}
if (newSquareRoot.compareTo(squareRoot) == 0) {
return false;
}
squareRoot = newSquareRoot;
square = squareRoot.multiply(squareRoot);
comparison = square.compareTo(num);
}
return true;
}
}
