web-dev-qa-db-ja.com

ブースト正規分布クラスの使用方法は？

平均0とシグマ1の正規分布を生成するために、boost :: normal_distributionを使用しようとしています。

次のコードは、一部の値が-1および1を超えているため、機能しません（また、そうではないはずです）。私が間違っていることを誰かが指摘できますか？

#include <boost/random.hpp>
#include <boost/random/normal_distribution.hpp>

int main()
{
  boost::mt19937 rng; // I don't seed it on purpouse (it's not relevant)

  boost::normal_distribution<> nd(0.0, 1.0);

  boost::variate_generator<boost::mt19937&, 
                           boost::normal_distribution<> > var_nor(rng, nd);

  int i = 0; for (; i < 10; ++i)
  {
    double d = var_nor();
    std::cout << d << std::endl;
  }
}

私のマシンでの結果は次のとおりです。

0.213436
-0.49558
1.57538
-1.0592
1.83927
1.88577
0.604675
-0.365983
-0.578264
-0.634376

ご覧のとおり、すべての値が-1から1の間ではありません。

よろしくお願いします！

[〜＃〜] edit [〜＃〜]：これは、締め切りがあり、練習をする前に理論を勉強することを避けたときに起こることです。

c++booststatisticsnormal-distribution
24
davidag

次のコードは、一部の値が-1および1を超えているため、機能しません（また、そうではないはずです）。私が間違っていることを誰かが指摘できますか？

いいえ、これは標準偏差（コンストラクターの2番目のパラメーター）の誤解です。1）正規分布の。

正規分布は、おなじみのベルカーブです。その曲線は、値の分布を効果的に示しています。ベルカーブのピークに近い値は、遠くにある値（分布の裾）よりも可能性が高くなります。

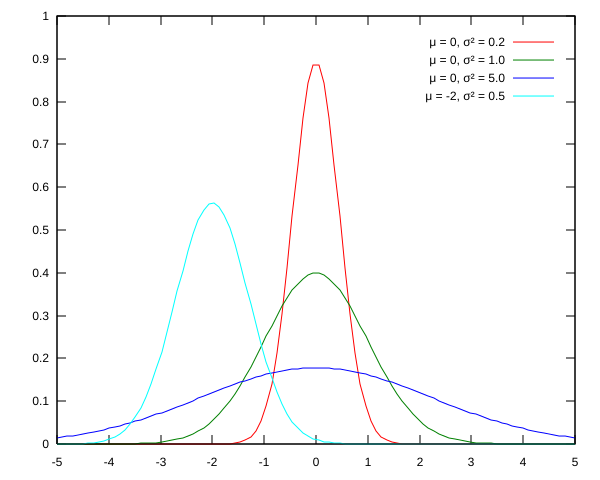
標準偏差は、値がどの程度広がっているかを示します。数値が小さいほど、平均値の周りに集中した値があります。数値が大きいほど、平均値の周りの集中度が低くなります。下の画像では、赤い曲線の分散（分散は標準偏差の2乗）が0.2であることがわかります。これを、平均は同じですが分散が1.0の緑色の曲線と比較してください。緑の曲線の値は、赤の曲線に比べてより広がっていることがわかります。紫色の曲線の分散は5.0で、値はさらに分散しています。

したがって、これは、値が_[-1, 1]_に限定されない理由を説明しています。ただし、値の68％が常に平均の1標準偏差内にあることは興味深い事実です。したがって、自分にとって興味深いテストとして、平均が0で分散が1の正規分布から多数の値を抽出し、平均の1標準偏差内にある数を数えるプログラムを作成します。 68％に近い数値が得られるはずです（もう少し正確には68.2689492137％）。

alt text

1：ブーストから ドキュメント ：

normal_distribution(RealType mean = 0, RealType sd = 1);

平均平均と標準偏差sdで正規分布を作成します。

30
jason

あなたは何も悪いことをしていません。正規分布の場合、シグマは範囲ではなく標準偏差を指定します。十分なサンプルを生成すると、それらの約68％のみが[平均-シグマ、平均+シグマ]の範囲内にあり、約95％が2シグマ内にあり、99％以上が3シグマ内にあることがわかります。

8
Jim Lewis