これは、正の整数の階乗(非常に小さなサブセットですが)に対して機能します。
unsigned long factorial(unsigned long f)
{
if ( f == 0 )
return 1;
return(f * factorial(f - 1));
}
printf("%i", factorial(5));
問題の性質(および認めたレベル)により、このソリューションは、次の「置換エンジン」で使用される関数ではなく、これを解決するという概念に基づいています。
これは、ULONG_MAXまでの非負の整数の階乗を計算します。*桁数が非常に多いため、計算する時間がある場合でも、マシンがさらに多くを保存することはできません。リンクする必要があるGNU多精度ライブラリを使用します。
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
#include <gmp.h>
void factorial(mpz_t result, unsigned long input) {
mpz_set_ui(result, 1);
while (input > 1) {
mpz_mul_ui(result, result, input--);
}
}
int main() {
mpz_t fact;
unsigned long input = 0;
char *buf;
mpz_init(fact);
scanf("%lu", &input);
factorial(fact, input);
buf = malloc(mpz_sizeinbase(fact, 10) + 1);
assert(buf);
mpz_get_str(buf, 10, fact);
printf("%s\n", buf);
free(buf);
mpz_clear(fact);
}
出力例:
$ make factorial CFLAGS="-L/bin/ -lcyggmp-3 -pedantic" -B && ./factorial
cc -L/bin/ -lcyggmp-3 -pedantic factorial.c -o factorial
100
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
[*]「番号」で他のことを意味する場合は、より具体的にする必要があります。ガンマ関数を使用してドメインを拡張するPascalの勇敢な努力にもかかわらず、階乗が定義されている他の数値は知りません。
Haskellで できるときにCでそれを行う理由 :
フレッシュマンハスケルプログラマー
fac n = if n == 0
then 1
else n * fac (n-1)
2年生のHaskellプログラマ、MIT(Schemeを新入生として研究)
fac = (\(n) ->
(if ((==) n 0)
then 1
else ((*) n (fac ((-) n 1)))))
ジュニアHaskellプログラマー(Peanoプレイヤーから開始)
fac 0 = 1
fac (n+1) = (n+1) * fac n
別のジュニアHaskellプログラマー(n + kパターンは「Haskellの嫌な部分」 1 であり、「Ban n + kパターン」の動きに加わった[2])
fac 0 = 1
fac n = n * fac (n-1)
シニアHaskellプログラマー(ニクソンブキャナンブッシュに投票—「リーズライト」)
fac n = foldr (*) 1 [1..n]
別の上級Haskellプログラマー(McGovern Biafra Naderに投票—「左寄り」)
fac n = foldl (*) 1 [1..n]
さらに別の上級Haskellプログラマー(これまで右に傾いたので、彼は再び左に戻ってきました!)
-- using foldr to simulate foldl
fac n = foldr (\x g n -> g (x*n)) id [1..n] 1
Haskellプログラマーのメモ(毎日のイチョウ葉巻)
facs = scanl (*) 1 [1..]
fac n = facs !! n
無意味な(ahem)「ポイントフリー」のHaskellプログラマー(オックスフォードで勉強)
fac = foldr (*) 1 . enumFromTo 1
反復型Haskellプログラマー(元Pascalプログラマー)
fac n = result (for init next done)
where init = (0,1)
next (i,m) = (i+1, m * (i+1))
done (i,_) = i==n
result (_,m) = m
for i n d = until d n i
反復ワンライナーHaskellプログラマー(以前のAPLおよびCプログラマー)
fac n = snd (until ((>n) . fst) (\(i,m) -> (i+1, i*m)) (1,1))
Haskellプログラマーの蓄積(迅速なクライマックスまで構築)
facAcc a 0 = a
facAcc a n = facAcc (n*a) (n-1)
fac = facAcc 1
継続的なHaskellプログラマー(初期にRABBITSを育て、その後ニュージャージーに移った)
facCps k 0 = k 1
facCps k n = facCps (k . (n *)) (n-1)
fac = facCps id
ボーイスカウトハスケルプログラマー(結び目を結ぶのが好き。常に「敬虔」であり、彼は最小固定小数点教会[8]に所属)
y f = f (y f)
fac = y (\f n -> if (n==0) then 1 else n * f (n-1))
組み合わせ型Haskellプログラマー(難読化されていない場合でも変数を避けます。このカリー化は単なるフェーズですが、ほとんど妨げられません)
s f g x = f x (g x)
k x y = x
b f g x = f (g x)
c f g x = f x g
y f = f (y f)
cond p f g x = if p x then f x else g x
fac = y (b (cond ((==) 0) (k 1)) (b (s (*)) (c b pred)))
リストをエンコードするHaskellプログラマー(単項で数えることが望ましい)
arb = () -- "undefined" is also a good RHS, as is "arb" :)
listenc n = replicate n arb
listprj f = length . f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
解釈的Haskellプログラマー(彼が好きではない「言語に出会ったことはない」)
-- a dynamically-typed term language
data Term = Occ Var
| Use Prim
| Lit Integer
| App Term Term
| Abs Var Term
| Rec Var Term
type Var = String
type Prim = String
-- a domain of values, including functions
data Value = Num Integer
| Bool Bool
| Fun (Value -> Value)
instance Show Value where
show (Num n) = show n
show (Bool b) = show b
show (Fun _) = ""
prjFun (Fun f) = f
prjFun _ = error "bad function value"
prjNum (Num n) = n
prjNum _ = error "bad numeric value"
prjBool (Bool b) = b
prjBool _ = error "bad boolean value"
binOp inj f = Fun (\i -> (Fun (\j -> inj (f (prjNum i) (prjNum j)))))
-- environments mapping variables to values
type Env = [(Var, Value)]
getval x env = case lookup x env of
Just v -> v
Nothing -> error ("no value for " ++ x)
-- an environment-based evaluation function
eval env (Occ x) = getval x env
eval env (Use c) = getval c prims
eval env (Lit k) = Num k
eval env (App m n) = prjFun (eval env m) (eval env n)
eval env (Abs x m) = Fun (\v -> eval ((x,v) : env) m)
eval env (Rec x m) = f where f = eval ((x,f) : env) m
-- a (fixed) "environment" of language primitives
times = binOp Num (*)
minus = binOp Num (-)
equal = binOp Bool (==)
cond = Fun (\b -> Fun (\x -> Fun (\y -> if (prjBool b) then x else y)))
prims = [ ("*", times), ("-", minus), ("==", equal), ("if", cond) ]
-- a term representing factorial and a "wrapper" for evaluation
facTerm = Rec "f" (Abs "n"
(App (App (App (Use "if")
(App (App (Use "==") (Occ "n")) (Lit 0))) (Lit 1))
(App (App (Use "*") (Occ "n"))
(App (Occ "f")
(App (App (Use "-") (Occ "n")) (Lit 1))))))
fac n = prjNum (eval [] (App facTerm (Lit n)))
Static Haskellプログラマー(彼はクラスでそれをします、彼はそのファンダップジョーンズを手に入れました!Thomas Hallgrenの「Funs with Functional Dependencies」[7]の後)
-- static Peano constructors and numerals
data Zero
data Succ n
type One = Succ Zero
type Two = Succ One
type Three = Succ Two
type Four = Succ Three
-- dynamic representatives for static Peanos
zero = undefined :: Zero
one = undefined :: One
two = undefined :: Two
three = undefined :: Three
four = undefined :: Four
-- addition, a la Prolog
class Add a b c | a b -> c where
add :: a -> b -> c
instance Add Zero b b
instance Add a b c => Add (Succ a) b (Succ c)
-- multiplication, a la Prolog
class Mul a b c | a b -> c where
mul :: a -> b -> c
instance Mul Zero b Zero
instance (Mul a b c, Add b c d) => Mul (Succ a) b d
-- factorial, a la Prolog
class Fac a b | a -> b where
fac :: a -> b
instance Fac Zero One
instance (Fac n k, Mul (Succ n) k m) => Fac (Succ n) m
-- try, for "instance" (sorry):
--
-- :t fac four
卒業生のHaskellプログラマー(大学院教育では、ハードウェアベースの整数の効率などについてのささいな心配事から解放される傾向があります)
-- the natural numbers, a la Peano
data Nat = Zero | Succ Nat
-- iteration and some applications
iter z s Zero = z
iter z s (Succ n) = s (iter z s n)
plus n = iter n Succ
mult n = iter Zero (plus n)
-- primitive recursion
primrec z s Zero = z
primrec z s (Succ n) = s n (primrec z s n)
-- two versions of factorial
fac = snd . iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
デカルトに傾いたHaskellプログラマー(ギリシャ料理を好み、辛いインド料理を避けます。LexAugusteijnの「ソートモーフィズム」[3]に触発されました)
-- (product-based, list) catamorphisms and an application
cata (n,c) [] = n
cata (n,c) (x:xs) = c (x, cata (n,c) xs)
mult = uncurry (*)
prod = cata (1, mult)
-- (co-product-based, list) anamorphisms and an application
ana f = either (const []) (cons . pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
博士Haskellプログラマー(非常に多くのバナナを食べたので目が狂ったようになりましたが、今では新しいレンズが必要です!)
-- explicit type recursion based on functors
newtype Mu f = Mu (f (Mu f)) deriving Show
in x = Mu x
out (Mu x) = x
-- cata- and ana-morphisms, now for *arbitrary* (regular) base functors
cata phi = phi . fmap (cata phi) . out
ana psi = in . fmap (ana psi) . psi
-- base functor and data type for natural numbers,
-- using a curried elimination operator
data N b = Zero | Succ b deriving Show
instance Functor N where
fmap f = nelim Zero (Succ . f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi . fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr . cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
在任中の教授(新入生にHaskellを教える)
fac n = product [1..n]
クリストフのおかげで、かなりの数の「数値」で機能するC99ソリューション:
#include <math.h>
#include <stdio.h>
double fact(double x)
{
return tgamma(x+1.);
}
int main()
{
printf("%f %f\n", fact(3.0), fact(5.0));
return 0;
}
6.000000 120.000000を生成します
大きなnの場合、いくつかの問題が発生する可能性があり、スターリングの近似を使用することができます。
これは:
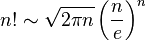
あなたの主な目的が興味深い外観の機能である場合:
int facorial(int a) {
int b = 1, c, d, e;
a--;
for (c = a; c > 0; c--)
for (d = b; d > 0; d--)
for (e = c; e > 0; e--)
b++;
return b;
}
(実際の使用のためのアルゴリズムとしては推奨されません。)
C99(またはJava)では、階乗関数を次のように繰り返し記述します。
int factorial(int n)
{
int result = 1;
for (int i = 2; i <= n; i++)
{
result *= i;
}
return result;
}
Cは関数型言語ではないため、末尾呼び出しの最適化に依存することはできません。したがって、必要がない限り、C(またはJava)で再帰を使用しないでください。
階乗が再帰の最初の例としてよく使用されるからといって、それを計算するために再帰が必要なわけではありません。
C(およびJava)のカスタムのように、nが大きすぎる場合、これは警告なしにオーバーフローします。
Intが表すことができる数値が、計算する階乗に対して小さすぎる場合は、別の数値タイプを選択します。 long longが少しだけ大きい場合は、floatまたはdoubleが必要です(nが大きすぎず、不正確でなくてもかまいません)。本当に大きな階乗の正確な値が必要な場合は、大きな整数。
末尾再帰バージョン:
long factorial(long n)
{
return tr_fact(n, 1);
}
static long tr_fact(long n, long result)
{
if(n==1)
return result;
else
return tr_fact(n-1, n*result);
}
OPENSSLのBIGNUM実装を使用するCプログラムを次に示します。したがって、学生には特に役立ちません。 (もちろん、BIGNUMを入力パラメーターとして受け入れるのはおかしいですが、BIGNUM間の相互作用を示すのに役立ちます)。
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <openssl/crypto.h>
#include <openssl/bn.h>
BIGNUM *factorial(const BIGNUM *num)
{
BIGNUM *count = BN_new();
BIGNUM *fact = NULL;
BN_CTX *ctx = NULL;
BN_one(count);
if( BN_cmp(num, BN_value_one()) <= 0 )
{
return count;
}
ctx = BN_CTX_new();
fact = BN_dup(num);
BN_sub(count, fact, BN_value_one());
while( BN_cmp(count, BN_value_one()) > 0 )
{
BN_mul(fact, count, fact, ctx);
BN_sub(count, count, BN_value_one());
}
BN_CTX_free(ctx);
BN_free(count);
return fact;
}
このテストプログラムは、入力用の数値の作成方法と戻り値の処理方法を示しています。
int main(int argc, char *argv[])
{
const char *test_cases[] =
{
"0", "1",
"1", "1",
"4", "24",
"15", "1307674368000",
"30", "265252859812191058636308480000000",
"56", "710998587804863451854045647463724949736497978881168458687447040000000000000",
NULL, NULL
};
int index = 0;
BIGNUM *bn = NULL;
BIGNUM *fact = NULL;
char *result_str = NULL;
for( index = 0; test_cases[index] != NULL; index += 2 )
{
BN_dec2bn(&bn, test_cases[index]);
fact = factorial(bn);
result_str = BN_bn2dec(fact);
printf("%3s: %s\n", test_cases[index], result_str);
assert(strcmp(result_str, test_cases[index + 1]) == 0);
OPENSSL_free(result_str);
BN_free(fact);
BN_free(bn);
bn = NULL;
}
return 0;
}
Gccでコンパイル:
gcc factorial.c -o factorial -g -lcrypto
int factorial(int n){
return n <= 1 ? 1 : n * factorial(n-1);
}
#Newbie programmer
def factorial(x):
if x == 0:
return 1
else:
return x * factorial(x - 1)
print factorial(6)
#First year programmer, studied Pascal
def factorial(x):
result = 1
i = 2
while i <= x:
result = result * i
i = i + 1
return result
print factorial(6)
#First year programmer, studied C
def fact(x): #{
result = i = 1;
while (i <= x): #{
result *= i;
i += 1;
#}
return result;
#}
print(fact(6))
#First year programmer, SICP
@tailcall
def fact(x, acc=1):
if (x > 1): return (fact((x - 1), (acc * x)))
else: return acc
print(fact(6))
#First year programmer, Python
def Factorial(x):
res = 1
for i in xrange(2, x + 1):
res *= i
return res
print Factorial(6)
#Lazy Python programmer
def fact(x):
return x > 1 and x * fact(x - 1) or 1
print fact(6)
#Lazier Python programmer
f = lambda x: x and x * f(x - 1) or 1
print f(6)
#Python expert programmer
import operator as op
import functional as f
fact = lambda x: f.foldl(op.mul, 1, xrange(2, x + 1))
print fact(6)
#Python hacker
import sys
@tailcall
def fact(x, acc=1):
if x: return fact(x.__sub__(1), acc.__mul__(x))
return acc
sys.stdout.write(str(fact(6)) + '\n')
#EXPERT PROGRAMMER
import c_math
fact = c_math.fact
print fact(6)
#ENGLISH EXPERT PROGRAMMER
import c_maths
fact = c_maths.fact
print fact(6)
#Web designer
def factorial(x):
#-------------------------------------------------
#--- Code snippet from The Math Vault ---
#--- Calculate factorial (C) Arthur Smith 1999 ---
#-------------------------------------------------
result = str(1)
i = 1 #Thanks Adam
while i <= x:
#result = result * i #It's faster to use *=
#result = str(result * result + i)
#result = int(result *= i) #??????
result str(int(result) * i)
#result = int(str(result) * i)
i = i + 1
return result
print factorial(6)
#Unix programmer
import os
def fact(x):
os.system('factorial ' + str(x))
fact(6)
#Windows programmer
NULL = None
def CalculateAndPrintFactorialEx(dwNumber,
hOutputDevice,
lpLparam,
lpWparam,
lpsscSecurity,
*dwReserved):
if lpsscSecurity != NULL:
return NULL #Not implemented
dwResult = dwCounter = 1
while dwCounter <= dwNumber:
dwResult *= dwCounter
dwCounter += 1
hOutputDevice.write(str(dwResult))
hOutputDevice.write('\n')
return 1
import sys
CalculateAndPrintFactorialEx(6, sys.stdout, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL)
#Enterprise programmer
def new(cls, *args, **kwargs):
return cls(*args, **kwargs)
class Number(object):
pass
class IntegralNumber(int, Number):
def toInt(self):
return new (int, self)
class InternalBase(object):
def __init__(self, base):
self.base = base.toInt()
def getBase(self):
return new (IntegralNumber, self.base)
class MathematicsSystem(object):
def __init__(self, ibase):
Abstract
@classmethod
def getInstance(cls, ibase):
try:
cls.__instance
except AttributeError:
cls.__instance = new (cls, ibase)
return cls.__instance
class StandardMathematicsSystem(MathematicsSystem):
def __init__(self, ibase):
if ibase.getBase() != new (IntegralNumber, 2):
raise NotImplementedError
self.base = ibase.getBase()
def calculateFactorial(self, target):
result = new (IntegralNumber, 1)
i = new (IntegralNumber, 2)
while i <= target:
result = result * i
i = i + new (IntegralNumber, 1)
return result
print StandardMathematicsSystem.getInstance(new (InternalBase, new (IntegralNumber, 2))).calculateFactorial(new (IntegralNumber, 6))
これを行うには、次のコードを使用します。
#include <stdio.h>
#include <stdlib.h>
int main()
{
int x, number, fac;
fac = 1;
printf("Enter a number:\n");
scanf("%d",&number);
if(number<0)
{
printf("Factorial not defined for negative numbers.\n");
exit(0);
}
for(x = 1; x <= number; x++)
{
if (number >= 0)
fac = fac * x;
else
fac=1;
}
printf("%d! = %d\n", number, fac);
}
私はほとんどの場合これを使用するとは思わないが、あまり広く使用されなくなっているよく知られている方法の1つは、ルックアップテーブルを使用することです。組み込み型のみを使用している場合、メモリヒットはわずかです。
もう1つのアプローチは、ポスターに別の手法を認識させることです。多くの再帰的ソリューションもメモ化できます。これにより、アルゴリズムの実行時にルックアップテーブルが入力され、将来の呼び出しのコストが大幅に削減されます(おそらく.NET JITコンパイルの背後にある原理のようなものです)。
大きな数の場合、tgammaがmath.hから(n!= Gamma(n + 1))を与える近似解でおそらく回避できます。さらに大きな数値が必要な場合、それらはdoubleに収まらないため、代わりにlgamma(ガンマ関数の自然対数)を使用する必要があります。
完全なC99 math.hなしでどこかで作業している場合は、このタイプのことを自分で簡単に行うことができます。
double logfactorial(int n) {
double fac = 0.0;
for ( ; n>1 ; n--) fac += log(fac);
return fac;
}
シンプルなソリューション:
unsigned int factorial(unsigned int n)
{
return (n == 1 || n == 0) ? 1 : factorial(n - 1) * n;
}
最も単純で効率的なのは、対数を合計することです。 Log10を使用すると、パワーと指数が得られます。
疑似コード
r=0
for i form 1 to n
r=r+log(i)/log(10)
print "result is:", 10^(r-floor(r)) ,"*10^" , floor(r)
整数部分が多くなりすぎて精度が低下しないようにコードを追加する必要がある場合がありますが、非常に大きな階乗でも結果は問題ありません。
1から指定した制限日nまで開始する必要があります。1*2*3...*nから開始します。
Cでは、関数として書いています。
main()
{
int n;
scanf("%d",&n);
printf("%ld",fact(n));
}
long int fact(int n)
{
long int facto=1;
int i;
for(i=1;i<=n;i++)
{
facto=facto*i;
}
return facto;
}
再帰を使用したCの例(Cはタグ付けされているので、それがあなたが望んでいることだと思います)
unsigned long factorial(unsigned long f)
{
if (f) return(f * factorial(f - 1));
return 1;
}
printf("%lu", factorial(5));
ジョンが言ったように、私は事前に計算されたルックアップテーブルを使用してこれを行います。これは、反復または再帰的なソリューションよりも計算が速くなります。最大のnであるため、n!の成長速度に依存しています。 unsigned long long(最大値18,446,744,073,709,551,615)をオーバーフローせずに計算できるのは20!だけなので、21要素の配列のみが必要です。これはcでどのように見えるかです。
long long factorial (int n) {
long long f[22] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, 87178291200, 1307674368000, 20922789888000, 355687428096000, 6402373705728000, 121645100408832000, 2432902008176640000, 51090942171709440000};
return f[n];
}
**I used this code for Factorial:**
#include<stdio.h>
int main(){
int i=1,f=1,n;
printf("\n\nEnter a number: ");
scanf("%d",&n);
while(i<=n){
f=f*i;
i++;
}
printf("Factorial of is: %d",f);
getch();
}