チップ内のトランジスタの数を増やすと、どのように速度が上がりますか?
CPUのトランジスタの唯一の目的は、その命令セットを定義するスイッチとして機能することですか?もしそうなら、なぜトランジスタの数を増やすとその速度が上がるのですか?
頭のてっぺんから:
もっと キャッシュ 、これはRAMよりも高速です
もっと SIMD命令 、単一データ命令よりも速く処理します
More cores なので、一度に2つ以上のことができます
組み込みの [〜#〜] fpu [〜#〜] s、複数の [〜#〜] alu [〜#〜] sなどのより機能的なユニット
パイプライン なので、各コアは一度により多くのことを実行できます
より洗練されたようなより良い処理ロジック 分岐予測 ロジック
この種のことに興味があるなら、NoamNisanとShimonSchockenによる本The Elements of Computingを強くお勧めします(少なくとも前半) 。それを通過した後、あなたは関係する部分の完全な理解であなた自身の質問に非常に詳細に答えることができるでしょう。
コンパニオンウェブサイト 実際にはいくつかのサンプルの章とメモがあります。とても親しみやすい本です。私は問題なく自分でそれを経験し、それからそれを主要なテキストとして使用する私の大学で真新しいクラスを受講しました。
簡単な答えは、トランジスタが増えても残りのトランジスタは動かないということですより速くですが、期間ごとに1つのことを行う代わりに、2つを行うことができます(いくつかの制限があります)。
ケンはすでにいくつかの理由を 彼の答え に要約しています。それをさらに拡張するには
- もっと キャッシュ 、これはRAMよりも高速です
明らかにより大きなキャッシュはより多くのトランジスタを必要とします。しかし、トランジスタが増えると、より高速なキャッシュを使用することもできます。 CPUキャッシュは [〜#〜] sram [〜#〜] で、通常は6つのトランジスタ(A.K.A 6T SRAM)で構成されています。ただし、十分な数のトランジスタがある場合は、6個を超えるトランジスタ(8T、10T SRAMなど)で作成された、より高速でより大きなSRAMセルを使用する価値がある場合があります。
- もっと SIMD命令 、単一データ命令よりも速く処理します
SIMDだけでなく、あらゆるタイプの加速命令。たとえば、最近のアーキテクチャには、暗号化/復号化を高速化するためのAESユニット、より優れた数学計算(特にデジタル信号処理)のための [〜#〜] fma [〜#〜] 、またはより高速な仮想マシンのための仮想化が備わっていることがよくあります。 。より多くの命令をサポートするということは、それらをデコードして実行するためにより多くのリソースが必要になることを意味します
これらは非常に明確です
- 組み込みの [〜#〜] fpu [〜#〜] s、複数の [〜#〜] alu [〜#〜] sなどのより機能的なユニット
以前は、FPUに十分なダイ領域がなかったため、浮動小数点演算の要件が高い場合は、別のダイ領域を購入する必要があります。大幅に多くのトランジスタを使用すると、FPUを組み込むことができ、浮動小数点演算を大幅に高速化できます。
その上、最近のCPUは スーパースカラー であり、独立していることを見つけることによって、一度に複数のことを実行しようとします命令ストリームが線形でシリアルであっても、データを前もって計算します。並行して実行できることが多ければ多いほど、高速になります。これを行うために、CPUは複数のALUを持つことができ、ALUは複数の実行ユニットを持つことができます。たとえば、CPUに前世代の4つと比較して5つの加算器がある場合、クロックを変更せずに最も楽観的な状況ですでに25%高速に実行されています。より洗練されたCPUは、 アウトオブオーダー実行 (ほとんどの最新の高性能CPUの場合)を採用しています。
- より洗練されたようなより良い処理ロジック 分岐予測 ロジック
通常、操作はさまざまな方法で実行できます。より多くのトランジスタがある場合は、より高速な手法を使用するためのより多くのリソースがあります。いくつかの簡単な例:
ビットシフト:
添加:
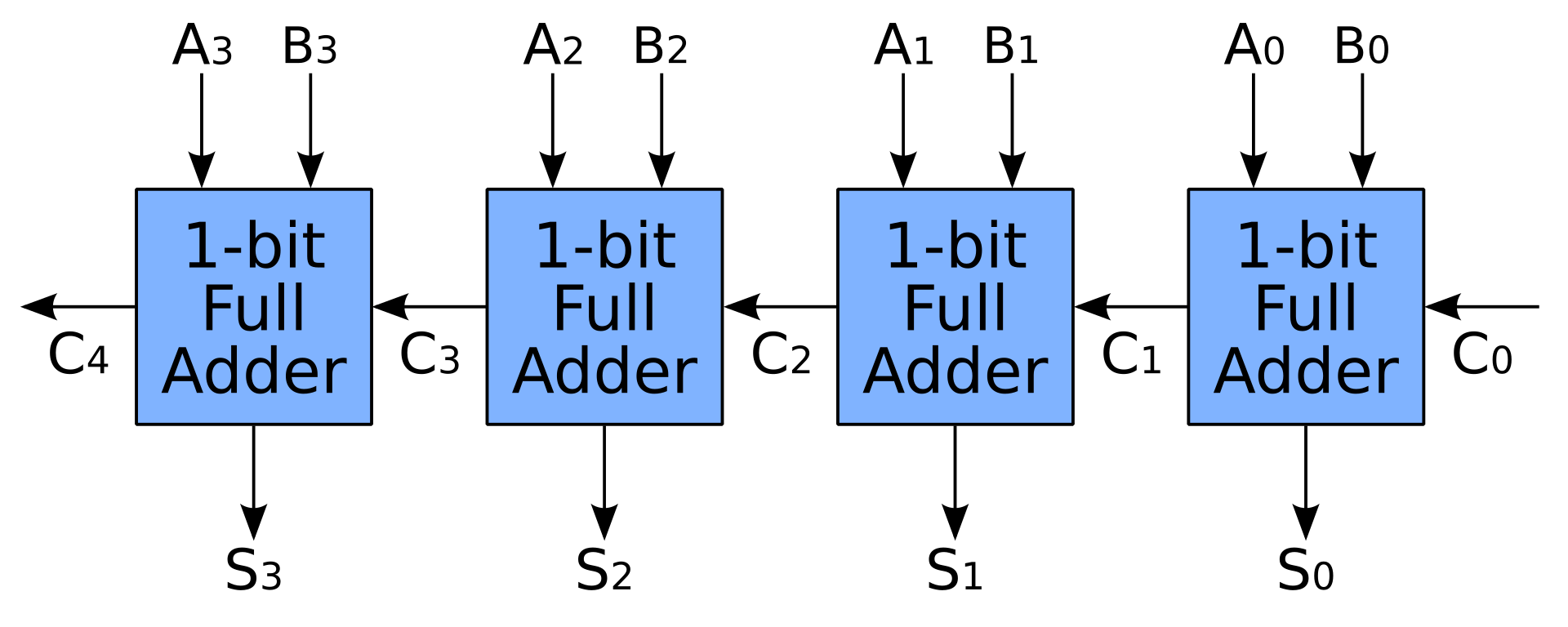
- 全加算器 を直列に接続することにより、単純な加算器も作成されます。このように、Nビット加算器はその仕事を完了するためにNクロックを必要としますが、これは確かに人々がCPUに期待するものではありません
![4-bit adder]()
- より多くのトランジスタを使用すると、 carry-lookahead または carry-save 加算器を使用してキャリーを事前計算することにより、加算を高速化できます。全加算器は引き続き使用されますが、キャリー事前計算ユニットにはさらに多くのスペースが必要です。
- 全加算器 を直列に接続することにより、単純な加算器も作成されます。このように、Nビット加算器はその仕事を完了するためにNクロックを必要としますが、これは確かに人々がCPUに期待するものではありません
同じことが、乗算器、除算器、スケジューラなどの他のユニットにも当てはまります。たとえば、 組み合わせロジック を使用すると、1つのクロックで非常に高速に乗算を実行できます。質問 ビット乗数-それらはどのように機能しますか? でいくつかの簡単な例を見ることができます。ただし、必要なトランジスタは入力幅の2乗に拡大するため、乗算器を備えた小さなCPUは、乗算器のスペースを大幅に節約するために、代わりに シーケンシャルロジック を使用します。
古い乗算器アーキテクチャでは、シフターとアキュムレータを使用して、各部分積(多くの場合、サイクルごとに1つの部分積)を合計し、速度とダイ面積をトレードオフしていました。最新の乗算器アーキテクチャでは、(変更された)Baugh-Wooleyアルゴリズム、ウォレスツリー、またはDadda乗算器を使用して、部分積を1つのサイクルで加算します。ウォレスツリーの実装のパフォーマンスは、2つの被乗数の1つをエンコードするブースを変更することで改善されることがあります。これにより、合計する必要のある部分積の数が減ります。
https://en.wikipedia.org/wiki/Binary_multiplier#Implementations
トランジスタの巨大なプールができたら、組み合わせロジックを使用して、乗数よりもはるかに多くのリソースを消費するFMAを実行することもできます。
最近のコンピュータには、組み合わせロジックで実装された乗算器と、それに続く加算器と結果を格納するアキュムレータレジスタで構成される専用のMACが含まれている場合があります。レジスタの出力は加算器の1つの入力にフィードバックされるため、各クロックサイクルで、乗算器の出力がレジスタに加算されます。組み合わせ乗算器は大量のロジックを必要としますが、以前のコンピューターで一般的なシフトと加算の方法よりもはるかに高速に積を計算できます。
トランジスタの数を増やすには、通常、トランジスタを小さくして、トランジスタを近づけ、信号の伝搬時間を短縮します。