楕円曲線暗号の使用
ランダムに生成されたキーの代わりに公開キーでデータを暗号化する方法でECCを使用できるかどうか疑問に思っています。
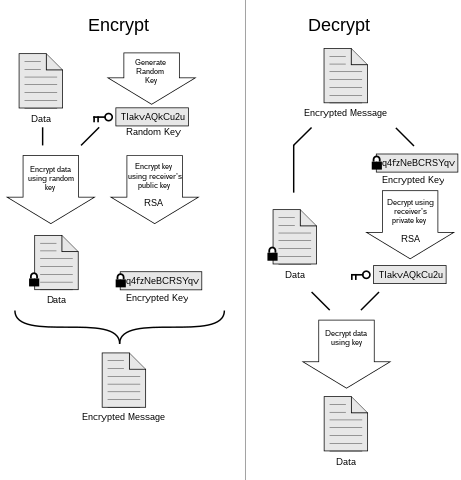
PGPが行うように、対称+非対称暗号化を一緒に使用する「従来の」方法と比較して、それを行う利点はありますか?.
ElGamal 非対称暗号化スキームは、楕円曲線に適用できます(実際、離散対数が難しい任意の有限グループで機能します)。ただし、これは、暗号化するデータを可逆的な方法で曲線ポイントにマッピングする必要があることを意味します。これは少しトリッキーです(これは実行可能ですが、より多くの数学が含まれるため、実装コードサイズが増加します)。ほとんどの場合、非対称暗号化を使用するため、実際には対称暗号化に使用されるセッションキーを暗号化する必要があります。楕円曲線上のDiffie-Hellmanキー交換は既にうまく機能しており、より簡単です(つまり、ECIESはDiffie-Hellmanです)。次に対称暗号化)。
ECCは、ランダムキーを暗号化してから、そのランダムキーを使用してデータを対称的に暗号化する代わりに、公開キーを使用してデータ自体を暗号化するために使用できます。しかし、これは Thomas Porninの回答 から PGPでは、受信者の公開キーでメッセージを暗号化しないのはなぜですか?なぜメタ暗号化なのですか? で説明されているように、これは良いアイデアではありません。
いずれの場合でも [〜#〜] ecies [〜#〜] は対称暗号化アルゴリズムを使用して実際にデータを暗号化するため、ECCを使用してすべてのデータを暗号化しても、まだ暗号化していますランダム対称鍵を使用します。しかし、ECIESを使用してデータ自体を暗号化する場合は、対称暗号化アルゴリズムとして単純なXOR=を使用できます。これは、実質的にワンタイムパッドです。これには、理論的な利点があります。他の対称暗号化アルゴリズムとは異なり、ワンタイムパッドは情報理論上安全です。