遺伝的アルゴリズムにおけるルーレットの選択
ルーレット選択機能に疑似コードを提供できる人はいますか?これをどのように実装しますか:
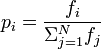
この数学の表記の読み方がよくわかりません。私は確率や統計を取ったことがありません。
私がこれを自分で行ってから数年になりますが、次の疑似コードはグーグルで簡単に見つかりました。
人口のすべてのメンバーについて 合計+ =この個人の適合度 終了 人口のすべてのメンバーについて 確率=確率の合計+(適合度/合計) 確率の合計+ =確率 for for ループは新しい母集団がいっぱいになるまで 行うこの2倍 数=母集団のすべてのメンバーに対して0〜1の間のランダム 数>確率であるが次の確率 未満の場合、あなたは選択されています 終了 終了 子孫を作成 ループ終了
これが発生したサイトは、詳細が必要な場合は here にあります。
すでに正しい解決策はたくさんありますが、このコードの方がわかりやすいと思います。
def select(fs):
p = random.uniform(0, sum(fs))
for i, f in enumerate(fs):
if p <= 0:
break
p -= f
return i
さらに、fsを累積すると、より効率的なソリューションを生成できます。
cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]
def select(cfs):
return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))
これはどちらも速く、非常に簡潔なコードです。 C++のSTLには、使用している言語であれば同様の二分法アルゴリズムが用意されています。
投稿された疑似コードには不明確な要素が含まれており、純粋な選択を実行する代わりにoffspringを生成する複雑さを追加します。ここに単純なpythonその擬似コードの実装があります:
def roulette_select(population, fitnesses, num):
""" Roulette selection, implemented according to:
<http://stackoverflow.com/questions/177271/roulette
-selection-in-genetic-algorithms/177278#177278>
"""
total_fitness = float(sum(fitnesses))
rel_fitness = [f/total_fitness for f in fitnesses]
# Generate probability intervals for each individual
probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
# Draw new population
new_population = []
for n in xrange(num):
r = Rand()
for (i, individual) in enumerate(population):
if r <= probs[i]:
new_population.append(individual)
break
return new_population
これは、確率的受け入れによるルーレットホイール選択と呼ばれます。
/// \param[in] f_max maximum fitness of the population
///
/// \return index of the selected individual
///
/// \note Assuming positive fitness. Greater is better.
unsigned rw_selection(double f_max)
{
for (;;)
{
// Select randomly one of the individuals
unsigned i(random_individual());
// The selection is accepted with probability fitness(i) / f_max
if (uniform_random_01() < fitness(i) / f_max)
return i;
}
}
1つの選択に必要な平均試行回数は次のとおりです。
τ= f最高 /平均(f)
- f最高 人口の最大適応度です
- avg(f)は平均フィットネスです
τは母集団の個体数(N)に明示的には依存しませんが、比率はNとともに変化する可能性があります。
ただし、多くのアプリケーション(フィットネスが制限されたままであり、平均フィットネスがNの増加に対して0に減少しない場合)では、τはNで無制限に増加しないため、このアルゴリズムの一般的な複雑さはO(1)(検索アルゴリズムを使用したルーレットホイールの選択には、O(N)またはO(log N)の複雑さがあります)。
この手順の確率分布は確かに、古典的なルーレットホイールの選択と同じです。
詳細については、以下を参照してください。
- 確率的受け入れによるルーレットホイールの選択(Adam Liposki、Dorota Lipowska-2011)
Cのコードは次のとおりです。
// Find the sum of fitnesses. The function fitness(i) should
//return the fitness value for member i**
float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
sumFitness += fitness(i);
// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(Rand() % 10000) / 9999.0f) * sumFitness;
// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;
while (randomNumber > partialSum)
{
partialSum += fitness(memberID);
memberID++;
}
**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**
スタンフォードAIラボのThrun教授も、UdacityのCS373の最中にpython=)で高速(er?)リサンプリングコードを発表しました。
http://www.udacity-forums.com/cs373/questions/20194/fast-resampling-algorithm
お役に立てれば
MatLabでのルーレットホイールの選択:
TotalFitness=sum(Fitness);
ProbSelection=zeros(PopLength,1);
CumProb=zeros(PopLength,1);
for i=1:PopLength
ProbSelection(i)=Fitness(i)/TotalFitness;
if i==1
CumProb(i)=ProbSelection(i);
else
CumProb(i)=CumProb(i-1)+ProbSelection(i);
end
end
SelectInd=Rand(PopLength,1);
for i=1:PopLength
flag=0;
for j=1:PopLength
if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
flag=1;
break;
end
end
if(flag==0)
SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
end
end
上記の回答から、私は次の結果を得ました。これは、回答自体よりも明確でした。
例を挙げましょう:
Random(sum):: Random(12)母集団を反復処理して、以下をチェックします:random <sum
乱数として7を選択します。
Index | Fitness | Sum | 7 < Sum
0 | 2 | 2 | false
1 | 3 | 5 | false
2 | 1 | 6 | false
3 | 4 | 10 | true
4 | 2 | 12 | ...
この例では、最も適合する(インデックス3)が、選択される割合(33%)が最も高くなっています。乱数は6-> 10の範囲内で着地する必要があるため、その乱数が選択されます。
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
}
double Rand = (((double)Rand() / (double)Rand_MAX) * sum);
sum = 0;
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
if (Rand < sum) {
//breed i
break;
}
}
これはコンパクトなJava実装であり、ルーレットの選択のために最近書いたものです。
public static gene rouletteSelection()
{
float totalScore = 0;
float runningScore = 0;
for (gene g : genes)
{
totalScore += g.score;
}
float rnd = (float) (Math.random() * totalScore);
for (gene g : genes)
{
if ( rnd>=runningScore &&
rnd<=runningScore+g.score)
{
return g;
}
runningScore+=g.score;
}
return null;
}
Based on my research ,Here is another implementation in C# if there is a need for it:
//those with higher fitness get selected wit a large probability
//return-->individuals with highest fitness
private int RouletteSelection()
{
double randomFitness = m_random.NextDouble() * m_totalFitness;
int idx = -1;
int mid;
int first = 0;
int last = m_populationSize -1;
mid = (last - first)/2;
// ArrayList's BinarySearch is for exact values only
// so do this by hand.
while (idx == -1 && first <= last)
{
if (randomFitness < (double)m_fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > (double)m_fitnessTable[mid])
{
first = mid;
}
mid = (first + last)/2;
// lies between i and i+1
if ((last - first) == 1)
idx = last;
}
return idx;
}
ルーレットホイールの選択の実装には2つの方法があります:Usualおよび確率的受け入れ1つ。
通常のアルゴリズム:
# there will be some amount of repeating organisms here.
mating_pool = []
all_organisms_in_population.each do |organism|
organism.fitness.times { mating_pool.Push(organism) }
end
# [very_fit_organism, very_fit_organism, very_fit_organism, not_so_fit_organism]
return mating_pool.sample #=> random, likely fit, parent!
確率的受け入れアルゴリズム:
max_fitness_in_population = all_organisms_in_population.sort_by(:fitness)[0]
loop do
random_parent = all_organisms_in_population.sample
probability = random_parent.fitness/max_fitness_in_population * 100
# if random_parent's fitness is 90%,
# it's very likely that Rand(100) is smaller than it.
if Rand(100) < probability
return random_parent #=> random, likely fit, parent!
else
next #=> or let's keep on searching for one.
end
end
どちらを選択しても、同じ結果が返されます。
役立つリソース:
http://natureofcode.com/book/chapter-9-the-evolution-of-code -遺伝的アルゴリズムに関する初心者にわかりやすい明確な章。 ルーレットホイールの選択を木製の文字のバケツとして説明します(入力が多いほど、Aを選ぶチャンスが大きいので、通常アルゴリズム)。
https://en.wikipedia.org/wiki/Fitness_proportionate_selection -確率的受け入れアルゴリズムについて説明します。
このSwift 4配列拡張は、重み付けされたランダム選択、つまりその要素からのルーレット選択を実装します。
_public extension Array where Element == Double {
/// Consider the elements as weight values and return a weighted random selection by index.
/// a.k.a Roulette wheel selection.
func weightedRandomIndex() -> Int {
var selected: Int = 0
var total: Double = self[0]
for i in 1..<self.count { // start at 1
total += self[i]
if( Double.random(in: 0...1) <= (self[i] / total)) { selected = i }
}
return selected
}
}
_たとえば、2つの要素の配列があるとします。
_[0.9, 0.1]
_weightedRandomIndex()は、90%の場合はゼロを返し、10%の場合は1つを返します。
これはより完全なテストです:
_let weights = [0.1, 0.7, 0.1, 0.1]
var results = [Int:Int]()
let n = 100000
for _ in 0..<n {
let index = weights.weightedRandomIndex()
results[index] = results[index, default:0] + 1
}
for (key,val) in results.sorted(by: { a,b in weights[a.key] < weights[b.key] }) {
print(weights[key], Double(val)/Double(n))
}
_出力:
_0.1 0.09906
0.1 0.10126
0.1 0.09876
0.7 0.70092
_この答えは基本的に、Andrew Maoのここでの答えと同じです。 https://stackoverflow.com/a/15582983/74975